题目内容
(本小题满分14分)
一个几何体是由圆柱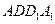 和三棱锥
和三棱锥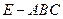 组合而成,点
组合而成,点 、
、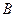 、
、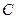 在圆
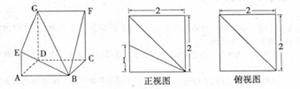
在圆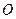 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中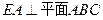 ,
,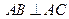 ,
,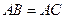 ,
,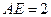 .
.
(1)求证: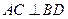 ;
;
(2)求三棱锥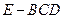 的体积.
的体积.
(本小题主要考查锥体体积,空间线线、线面关系,三视图等知识,考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.)
(1)证明:因为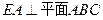 ,
,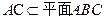 ,所以
,所以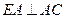 ,即
,即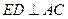 .
.
又因为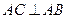 ,
,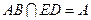 ,所以
,所以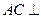 平面
平面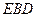 .
.
因为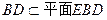 ,所以
,所以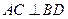 .………………………………………………………………4分
.………………………………………………………………4分
(2)解:因为点 、
、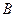 、
、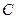 在圆
在圆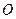 的圆周上,且
的圆周上,且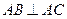 ,所以
,所以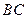 为圆
为圆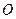 的直径.
的直径.
设圆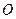 的半径为
的半径为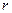 ,圆柱高为
,圆柱高为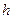 ,根据正(主)视图、侧(左)视图的面积可得,
,根据正(主)视图、侧(左)视图的面积可得,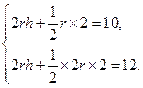 …………………………………………6分
…………………………………………6分
解得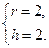
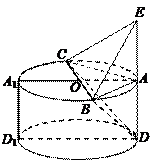
所以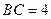 ,
,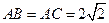 .………………………………………………………………………8分
.………………………………………………………………………8分
以下给出求三棱锥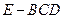 体积的两种方法:
体积的两种方法:
方法1:由(1)知,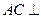 平面
平面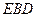 ,
,
所以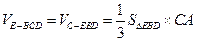 .………………………………………………………………10分
.………………………………………………………………10分
因为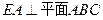 ,
,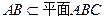 ,
,
所以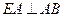 ,即
,即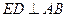 .
.
其中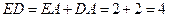 ,因为
,因为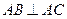 ,
,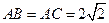 ,
,
所以 .…………………………………………………13分
.…………………………………………………13分
所以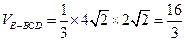 .…………………………………………………………………14分
.…………………………………………………………………14分
方法2:因为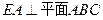 ,
,
所以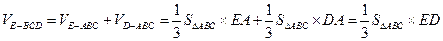 .…………………10分
.…………………10分
其中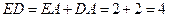 ,因为
,因为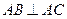 ,
,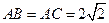 ,
,
所以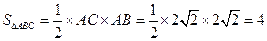 .…………………………………………………13分
.…………………………………………………13分
所以 .…………………………………………………………………………14分
.…………………………………………………………………………14分
解析

练习册系列答案
相关题目
 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
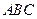 是边长为
是边长为 的等边三角形,
的等边三角形, 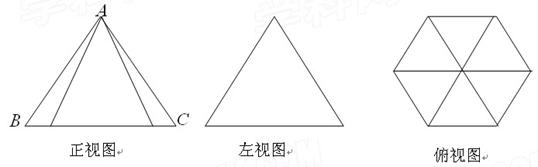
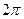 平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为
平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为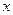 ,圆锥母线的长为
,圆锥母线的长为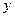
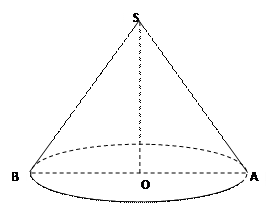
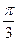 ,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)
,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)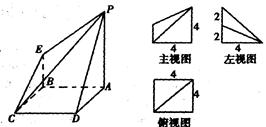
 一几何体的直观图、主视图、俯视图、左视图.
一几何体的直观图、主视图、俯视图、左视图.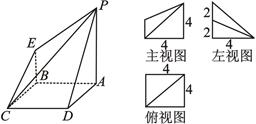
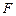 为
为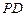 的中点,求证:
的中点,求证: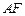
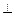 面
面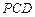 ;
;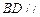 面
面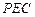 ;
;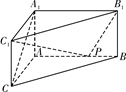
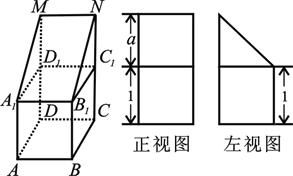
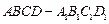 的上底面上叠放三棱柱
的上底面上叠放三棱柱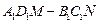 ,该几何体的正视图与左视图如右图所示.
,该几何体的正视图与左视图如右图所示.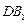
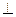
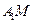 ,求实数
,求实数 的值;K^S*5U.C#O
的值;K^S*5U.C#O
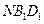 ;
; 所成角的正弦值
所成角的正弦值
 使得
使得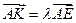 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为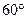 ,求
,求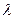 的值。
的值。