题目内容
设0<a,b,c<1,求证:(1-a)b,(1-b)c,(1-c)a不可能同时大于
思路分析:题目中出现了“不可能同时大于……”字样,而且三个式子的地位相同,结合0<(1-a)a≤[![]() ]2=
]2=![]() ,可得到方向相矛盾的两个不等式,适于用反证法.
,可得到方向相矛盾的两个不等式,适于用反证法.
证明:设(1-a)b>![]() ,(1-b)c>
,(1-b)c>![]() ,(1-c)a>
,(1-c)a>![]() ,
,
则三式相乘:(1-a)b·(1-b)c·(1-c)a>![]() .①
.①
又∵0<a,b,c<1,∴0<(1-a)a≤[![]() ]2=
]2=![]() .
.
同理:(1-b)b≤![]() ,(1-c)c≤
,(1-c)c≤![]() ,以上三式相乘:
,以上三式相乘:
(1-a)a·(1-b)b·(1-c)c≤![]() ,与①矛盾.∴原式成立.
,与①矛盾.∴原式成立.
巧解提示
凡涉及到证明不等式为否定性命题、唯一性命题或是含“至多”“至少”等字句时,可考虑使用反证法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
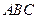 中,
中,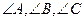 所对的边分别为
所对的边分别为 ,满足
,满足 成等差数列,
成等差数列, ,求点
,求点 的轨迹方程.
的轨迹方程. .
.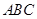 中,
中, 所对的边分别为
所对的边分别为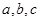 ,满足
,满足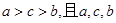 成等差数列,
成等差数列,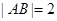 ,求点
,求点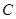 的轨迹方程.
的轨迹方程.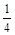 .
.