题目内容

6．现有5人坐成一排，任选其中3人相互调整位置（着3人中任何一人不能做回原来的位置），其余2人位置不变，则不同的调整的方案的种数有20．

分析 先考虑从5人中任选3人的方法数，再考虑3人位置全调的方法数，利用分步计数原理可求．

解答 解：从5人中任选3人有C53种，3人位置全调，由于不能是自己原来的位置，因此有A22种，故有C53A22=20种．
故答案为：20．

点评 本题主要考查排列组合知识，关键是问题的等价转化．

练习册系列答案
相关题目
16．已知0＜a≠1，函数f（x）=$\frac{4{a}^{x}+2}{{a}^{x}+1}$+xcosx（-1≤x≤1），设函数f（x）的最大值是M，最小值是N，则（　　）
A．M+N=8B．M+N=6C．M-N=8D．M-N=6
17．在△ABC中，AB=4，AC=8，∠BAC=60°，延长CB到D，使BA=BD，当E点在线段AD上移动时，若$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$，则t=λ-μ的最大值是$\frac{{3+2\sqrt{3}}}{3}$．
14．已知数列{an}、{bn}满足b1=an，bk-1bk=ak-1ak≠0，其中k=2，3，…，n，则称{bn}为{an}的“生成数列”．
（1）若数列a1，a2，a3，a4，a5的“生成数列”是1，2，3，4，5，求a1；
（2）若n为偶数，且{an}的“生成数列”是{bn}，证明：{bn}的“生成数列”是{an}；
（3）若n为奇数，且{an}的“生成数列”是{bn}，{bn}的“生成数列”是{cn}，…，依次将数列{an}，{bn}，{cn}，…的第i（i=1，2，…，n）项取出，构成数列Ωi：ai，bi，ci，…，．
探究：数列Ωi是否为等比数列，并说明理由．
1．已知集合A={x|x2-x≤0}，B={x|-2≤x≤0}，则A∩∁RB=（　　）
A．∅B．{x∈R|x≠0}C．{x|0＜x≤1}D．R
11．已知实数a＞1，若函数y=a${\;}^{\frac{x}{e}}$的图象与函数y=elogax的图象有两个不同的交点，则a的取值范围为（1，e）．
18．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=3，且（2$\overrightarrow{a}$-3$\overrightarrow{b}$）•（2$\overrightarrow{a}$+$\overrightarrow{b}$）=61，则向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为（　　）
A．30°B．60°C．120°D．150°
15．某班决定举行联欢会迎接元旦，小明负责游戏环节，他设计了一个“击球猜谜”的游戏，需要先在长为6米的绳子上挂上两个气球．
（1）若这两个小球挂在绳子的6等分点处，求两个气球相邻的概率；（两个气球不能挂在同一个等分点）．
（2）若其中一个气球挂在绳子的左起第一个三等分点处，求两个气球之间的距离不小于1米的概率．
16．据如图的流程图可得结果为（　　）
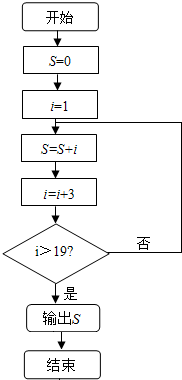
A．19B．67C．51D．70

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网