题目内容
已知函数f(x)=xlnx.
(1)求函数f(x)的单调区间和最小值;
(2)若函数F(x)=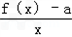 在[1,e]上是最小值为
在[1,e]上是最小值为 ,求a的值;
,求a的值;
(3)当b>0时,求证: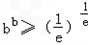 (其中e=2.718 28…是自然对数的底数).
(其中e=2.718 28…是自然对数的底数).
(1)求函数f(x)的单调区间和最小值;
(2)若函数F(x)=
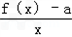 在[1,e]上是最小值为
在[1,e]上是最小值为 ,求a的值;
,求a的值;(3)当b>0时,求证:
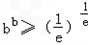 (其中e=2.718 28…是自然对数的底数).
(其中e=2.718 28…是自然对数的底数).(1)解:求导函数可得:f'(x)=lnx+1(x>0)
令f'(x)≥0,即lnx≥﹣1,∴x ;
;
令f'(x)≤0,即lnx≤﹣1,∴0<x ;
;
∴f(x)单调递增区间为[ ,+∞),单调递减区间为(0,
,+∞),单调递减区间为(0, ]
]
∴f(x)min=f( )=﹣
)=﹣
(2)解:F(x)= =
= ,求导函数可得
,求导函数可得
F'(x)=
当a≥0时,F'(x)>0,F(x)在[1,e]上单调递增,F(x)min=﹣a= ,
,
∴a=﹣
 [0,+∞),舍去;
[0,+∞),舍去;
当a<0时,F(x)在(0,﹣a)单调递减,在(﹣a,+∞)单调递增
若a∈(﹣1,0),F(x)在[1,e]上单调递增,F(x)min=﹣a= ,
,
∴a=﹣
 (﹣1,0),舍去;
(﹣1,0),舍去;
若a∈[﹣e,﹣1],F(x)在(1,﹣a)单调递减,在(﹣a,e)单调递增,
∴F(x)min=F(﹣a)=ln(﹣a)+1= ,
,
∴a=﹣ ∈[﹣e,﹣1];
∈[﹣e,﹣1];
若a∈(﹣∞,﹣1),F(x)在[1,e]上单调递减,
∴F(x)min=F(e)=﹣
 (﹣∞,﹣1),舍去;
(﹣∞,﹣1),舍去;
综上所述:a=﹣
(3)证明:由(1)可知当b>0时,有f(b)≥f(x)min=f( )=﹣
)=﹣ ,
,
∴ ,即
,即
 .
.
∴
令f'(x)≥0,即lnx≥﹣1,∴x
 ;
;令f'(x)≤0,即lnx≤﹣1,∴0<x
 ;
;∴f(x)单调递增区间为[
 ,+∞),单调递减区间为(0,
,+∞),单调递减区间为(0, ]
]∴f(x)min=f(
 )=﹣
)=﹣
(2)解:F(x)=
 =
= ,求导函数可得
,求导函数可得F'(x)=

当a≥0时,F'(x)>0,F(x)在[1,e]上单调递增,F(x)min=﹣a=
 ,
,∴a=﹣

 [0,+∞),舍去;
[0,+∞),舍去;当a<0时,F(x)在(0,﹣a)单调递减,在(﹣a,+∞)单调递增
若a∈(﹣1,0),F(x)在[1,e]上单调递增,F(x)min=﹣a=
 ,
,∴a=﹣

 (﹣1,0),舍去;
(﹣1,0),舍去;若a∈[﹣e,﹣1],F(x)在(1,﹣a)单调递减,在(﹣a,e)单调递增,
∴F(x)min=F(﹣a)=ln(﹣a)+1=
 ,
,∴a=﹣
 ∈[﹣e,﹣1];
∈[﹣e,﹣1];若a∈(﹣∞,﹣1),F(x)在[1,e]上单调递减,
∴F(x)min=F(e)=﹣

 (﹣∞,﹣1),舍去;
(﹣∞,﹣1),舍去;综上所述:a=﹣

(3)证明:由(1)可知当b>0时,有f(b)≥f(x)min=f(
 )=﹣
)=﹣ ,
,∴
 ,即
,即
 .
.∴


练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|