题目内容
在某次测验中,有6位同学的平均成绩为76分,用 表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
(1)求第6位同学的成绩 及这6位同学成绩的标准差s;
及这6位同学成绩的标准差s;
(2)从6位同学中随机地选2位同学,求恰有1位同学成绩在区间(70,75)中的概率.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:本题主要考查平均数、标准差、随机事件概率等基础知识,考查学生的计算能力.第一问,利用已知中给出的表格中的数据,代入到公式中直接求解,较简单;第二问,是随机事件的概率,列出所有事件的情况,在所有情况中数出符合题意的种数.
试题解析:(1)∵ ,
, ,
, ,∴
,∴ . 6分
. 6分
(2)从6位同学中随机选取2位同学,包含的基本事件空间为

 共15个基本事件,
共15个基本事件,
记“选出的2位同学中,恰有1位同学的成绩位于 ”为事件A,则事件A包含的基本事件为
”为事件A,则事件A包含的基本事件为
 ,共8个基本事件,则
,共8个基本事件,则 ,故从6位同学中随机地选2位同学,恰有1位同学的成绩位于
,故从6位同学中随机地选2位同学,恰有1位同学的成绩位于 的概率为
的概率为 . 12分
. 12分
考点:1.平均数;2.标准差;3.随机事件的概率.

练习册系列答案
相关题目
在某次高三考试成绩中,随机抽取了9位同学的数学成绩进行统计。下表是9位同学的选择题和填空题的得分情况(选择题满分60分,填空题满分16分):
| 选择题 | 40 | 55 | 50 | 45 | 50 | 40 | 45 | 60 | 40 |
| 填空题 | 12 | 16 |  | 12 | 16 | 12 | 8 | 12 | 8 |
 的值及他们填空题得分的标准差;
的值及他们填空题得分的标准差;(Ⅱ)在(1)的条件下,记这9位同学的选择题得分组成的集合为A,填空题得分组成的集合为B。若同学甲的解答题的得分是46分,现分别从集合A、B中各任取一个值当作其选择题和填空题的得分,求甲的数学成绩高于100分的概率。
下表是某单位在2013年1—5月份用水量(单位:百吨)的一组数据:
月份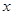 | 1 | 2 | 3 | 4 | 5 |
用水量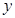 | 4 5 | 4 | 3 | 2 5 | 1 8 |
(Ⅰ)若由线性回归方程得到的预测数据与实际检验数据的误差不超过0 05,视为“预测可靠”,通过公式得
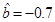 ,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;(Ⅱ)从这5个月中任取2个月的用水量,求所取2个月的用水量之和小于7(单位:百吨)的概率
参考公式:回归直线方程是:
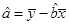 ,
,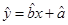
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000 株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
| | 高茎 | 矮茎 | 合计 |
| 圆粒 | 11 | 19 | 30 |
| 皱粒 | 13 | 7 | 20 |
| 合计 | 24 | 26 | 50 |
(2) 根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
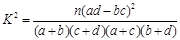 ,其中
,其中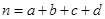 )
) 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
 =bx+a;
=bx+a;(2)试预测加工10个零件需要多少时间?
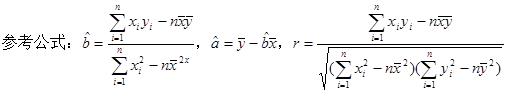
| n-2 | 1 | 2 | 3 | 4 |
| 小概率0.05 | 0.997 | 0.950 | 0.878 | 0.811 |
| 小概率0.01 | 1.000 | 0.990 | 0.959 | 0.917 |

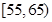 ,
,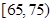 的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率.
的被调查者中各随机选取1人进行追踪调查,求两人中至少有1人赞成“车辆限行”的概率. 
 ,第2组
,第2组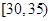 ,第3组
,第3组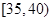 ,第4组
,第4组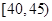 ,第5组
,第5组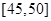 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
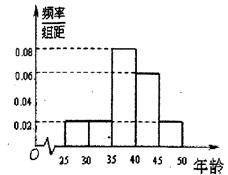
 的值;
的值;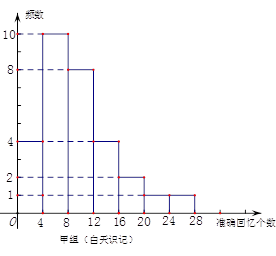
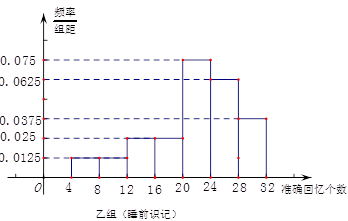
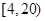 个范围内的学生中随机选2人,求能准确回忆
个范围内的学生中随机选2人,求能准确回忆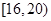 个单词至少有一人的概率.
个单词至少有一人的概率. 、第2组
、第2组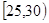 、第3组
、第3组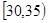 、第4组
、第4组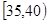 、第5组
、第5组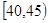 ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示: