题目内容
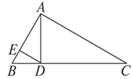
如图,在矩形ABCD中,AB> ·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设
·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设 =k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
=k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.

 ·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设
·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设 =k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
=k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
假设存在实数k的值,满足题设.
①先证明△AEF∽△DCE∽△ECF.因为EF⊥EC,
所以∠AEF=90°-∠DEC=∠DCE.
而∠A=∠D=90°,故△AEF∽△DCE.
故得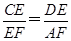 .又DE=EA,所以
.又DE=EA,所以 .
.
又∠CEF=∠EAF=90°,所以△AEF∽△ECF.
②再证明可以取到实数k的值,使△AEF∽△BCF,
由于∠AFE+∠BFC≠90°,故不可能有∠AFE=∠BFC,
因此要使△AEF∽△BCF,应有∠AFE=∠BFC,
此时,有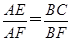 ,又AE=
,又AE= BC,故得AF=
BC,故得AF= BF=
BF=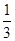 AB.
AB.
由△AEF∽△DCE,可知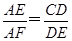 ,
,
因此,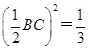 AB2,所以
AB2,所以 ,求得k=
,求得k=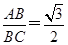 .
.
可以验证,当k=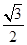 时,这四个三角形都是有一个锐角等于60°的直角三角形,故它们都相似.
时,这四个三角形都是有一个锐角等于60°的直角三角形,故它们都相似.
①先证明△AEF∽△DCE∽△ECF.因为EF⊥EC,
所以∠AEF=90°-∠DEC=∠DCE.
而∠A=∠D=90°,故△AEF∽△DCE.
故得
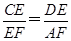 .又DE=EA,所以
.又DE=EA,所以 .
.又∠CEF=∠EAF=90°,所以△AEF∽△ECF.
②再证明可以取到实数k的值,使△AEF∽△BCF,
由于∠AFE+∠BFC≠90°,故不可能有∠AFE=∠BFC,
因此要使△AEF∽△BCF,应有∠AFE=∠BFC,
此时,有
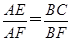 ,又AE=
,又AE= BC,故得AF=
BC,故得AF= BF=
BF=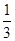 AB.
AB.由△AEF∽△DCE,可知
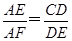 ,
,因此,
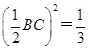 AB2,所以
AB2,所以 ,求得k=
,求得k=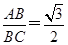 .
.可以验证,当k=
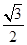 时,这四个三角形都是有一个锐角等于60°的直角三角形,故它们都相似.
时,这四个三角形都是有一个锐角等于60°的直角三角形,故它们都相似.
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
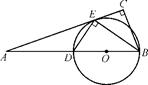
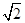 ,求BC的长.
,求BC的长.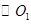 和
和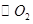 相交于A、B两点,过A点作
相交于A、B两点,过A点作
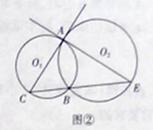
 求证:
求证:
 ;(2)
;(2) ∽
∽
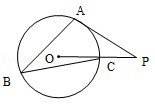
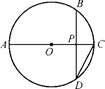


 中,
中, ,
, ,
, ,
, 、
、 为垂足,若AE=4,BE=1,则AC= .
为垂足,若AE=4,BE=1,则AC= .