Question

设X是一个离散型随机变量，其分布列如下表：

X	-1	0	1
P		1-2q	q2

(1)求q的值；

(2)求P(X＞-1).

Answer 1

解：(1)因为离散型随机变量的分布列满足：

①p_i≥0，i=1,2，…

②p₁+p₂+…=1，

所以有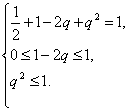

解得q=1-.

故X的分布列为：

X	-1	0	1
P		-1	-

(2)P(X＞-1)=P(X=0)+P(X=1)=-1+-=,或者P(X＞-1)=1-P(X=-1)=1-=.