题目内容
二阶矩阵M有特征值 ,其对应的一个特征向量e=
,其对应的一个特征向量e= ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成点
变换成点 .
.
(Ⅰ)求矩阵M;
(Ⅱ)求矩阵M的另一个特征值及对应的一个特征向量.
解:(Ⅰ)设M= ,则由
,则由
 =6
=6 得
得 =
= ,
,
即a+b=c+d=6. …………1分
由
 =
= ,得
,得 ,从而a+2b=8,c+2d=4. ……………2分
,从而a+2b=8,c+2d=4. ……………2分
由a+b =6及a+2b=8,解得a=4,b=2;
由c+d =6及c+2d=4,解得c=8,d=-2,
所以M= ……………3分
……………3分
(Ⅱ)由(Ⅰ)知矩阵 的特征多项式为
的特征多项式为
 ……………4分
……………4分
令 ,得矩阵
,得矩阵 的特征值为6与
的特征值为6与 . ……………5分
. ……………5分
当 时,
时, 
故矩阵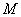 的属于另一个特征值
的属于另一个特征值 的一个特征向量为
的一个特征向量为 . ……………6分
. ……………6分

北京市各级各类中小学每年都要进行“学生体质健康测试”,测试总成绩满分为 分,规定测试成绩在
分,规定测试成绩在 之间为体质优秀;在
之间为体质优秀;在 之间为体质良好;在
之间为体质良好;在 之间为体质合格;在
之间为体质合格;在 之间为体质不合格.
之间为体质不合格.
现从某校高三年级的 名学生中随机抽取
名学生中随机抽取 名学生体质健康测试成绩,其茎叶图如下:
名学生体质健康测试成绩,其茎叶图如下:
| 9 | 1 | 3 | 5 | 6 | ||||||||||||
| 8 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 6 | 6 | 7 | 7 | 9 |
| 7 | 0 | 5 | 6 | 6 | 7 | 9 | ||||||||||
| 6 | 4 | 5 | 8 | |||||||||||||
| 5 | 6 |
(Ⅰ)试估计该校高三年级体质为优秀的学生人数;
(Ⅱ)根据以上 名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取
名学生体质健康测试成绩,现采用分层抽样的方法,从体质为优秀和良好的学生中抽取 名学生,再从这
名学生,再从这 名学生中选出
名学生中选出 人.
人.
(ⅰ)求在选出的 名学生中至少有
名学生中至少有 名体质为优秀的概率;
名体质为优秀的概率;
(ⅱ)记 为在选出的
为在选出的 名学生中体质为良好的人数,求
名学生中体质为良好的人数,求 的分布列及数学期望.
的分布列及数学期望.
甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如下表所示:
| 甲 | 乙 | 丙 | 丁 | |
| 平均环数 |
|
|
|
|
| 方差 |
|
|
|
|
从这四个人中选择一人参加奥运会射击项目比赛,最佳人选是
A.甲 B. 乙 C. 丙 D.丁
|
已知 与
与 之间的几组数据如下表:
之间的几组数据如下表:
|
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得线性回归直线方程为 .若某同学根据上表中前两组数据
.若某同学根据上表中前两组数据 和
和 求得的直线方程为
求得的直线方程为 ,则以下结论正确的是
,则以下结论正确的是
A. B.
B. C.
C. D.
D.
 的样本数据的频率分布直方图如图所示,则样本数据落在
的样本数据的频率分布直方图如图所示,则样本数据落在 内的样本频数为
内的样本频数为 A.
A. B.
B.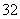 C.
C. D.
D.
 为坐标原点,动点
为坐标原点,动点 满足
满足 ,则点
,则点 是整数集
是整数集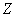 的非空子集,如果
的非空子集,如果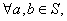 有
有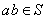 ,则称
,则称 ,
, 是
是 且
且 有
有 有
有 ,有四个命题:①
,有四个命题:① 中至少有一个关于乘法是封闭的;②
中至少有一个关于乘法是封闭的;②









 为纯虚数,那么实数
为纯虚数,那么实数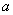 的值为( ).
的值为( ).  ,其中正确的是 ( )
,其中正确的是 ( ) (B)
(B) 
 (D)
(D) 