题目内容
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且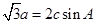 .
.
(1)确定角C的大小:
(2)若c=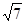 ,且△ABC的面积为
,且△ABC的面积为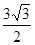
 ,求a+b的值.
,求a+b的值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)在三角形中,由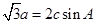 ,根据正弦定理得
,根据正弦定理得 ,知
,知 ;(2)由
;(2)由 ,得
,得 ,由余弦定理
,由余弦定理 ,又c=
,又c=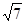 ,可得
,可得 ,所以
,所以 .
.
试题解析:解(1)由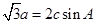 及正弦定理得,
及正弦定理得,
 4分
4分 是锐角三角形,
是锐角三角形, 7分
7分
(2)解法1: 由面积公式得,
由面积公式得, 10分
10分
由余弦定理得
由②变形得 14分
14分
解法2:前同解法1,联立①、②得 10分
10分
消去b并整理得 解得
解得
所以 故
故 14分
14分
考点:正、余弦定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,内角A,B,C的对边
中,内角A,B,C的对边 ,已知
,已知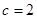 ,
,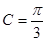 .
. ,求
,求 ;
;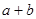 的取值范围.
的取值范围. 的内角
的内角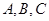 所对边的长分别是
所对边的长分别是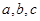 ,且
,且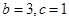 ,△
,△ ,求
,求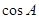 与
与 的值.
的值. 中,
中, ,
, ,
, .
.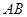 长;
长; 的值.
的值. ,并在点C测得塔顶A的仰角为
,并在点C测得塔顶A的仰角为 ,求塔高AB.
,求塔高AB.
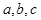 ,∠A、∠B、∠C的大小成等差数列,且
,∠A、∠B、∠C的大小成等差数列,且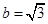
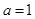 ,求∠A的大小;
,求∠A的大小;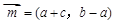 ,
,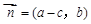 ,
,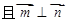 .
. ,求角A的值.
,求角A的值.
 +
+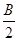 ),-1),且m⊥n.
),-1),且m⊥n.