题目内容
过点(1,0)直线l交抛物线y2=4x于A(x1,y1),B(x2,y2)两点,抛物线的顶点是O.
(ⅰ)证明: 为定值;
为定值;
(ⅱ)若AB中点横坐标为2,求AB的长度及l的方程.
证明:(ⅰ)设直线l的方程为x=my+1,代入y2=4x,得y2-4my-4=0,
∴y1y2=-4,∴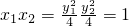 ,
,
∴ =x1x2+y1y2=-3为定值;
=x1x2+y1y2=-3为定值;
解:(ⅱ) l与X轴垂直时,AB中点横坐标不为2,
设直线l的方程为y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0,
∵AB中点横坐标为2,∴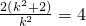 ,∴
,∴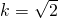 ,
,
l的方程为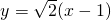 .
.
|AB|=x1+x2+2=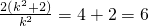 ,AB的长度为6.
,AB的长度为6.
分析:(ⅰ)利用直线l过点(1,0),可设直线l的方程为x=my+1,代入y2=4x,得y2-4my-4=0,利用韦达定理得关系式,再将向量用坐标表示,即可证得;
(ⅱ) 首先可知斜率存在,可设直线l的方程为y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0,根据AB中点横坐标为2,可得方程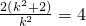 ,进而可求斜率,从而可求AB的长度及l的方程.
,进而可求斜率,从而可求AB的长度及l的方程.
点评:本题以抛物线为载体,考查直线与抛物线的位置关系,考查韦达定理的运用,有一定的综合性.
∴y1y2=-4,∴
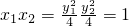 ,
,∴
 =x1x2+y1y2=-3为定值;
=x1x2+y1y2=-3为定值;解:(ⅱ) l与X轴垂直时,AB中点横坐标不为2,
设直线l的方程为y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0,
∵AB中点横坐标为2,∴
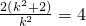 ,∴
,∴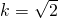 ,
,l的方程为
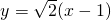 .
.|AB|=x1+x2+2=
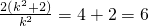 ,AB的长度为6.
,AB的长度为6.分析:(ⅰ)利用直线l过点(1,0),可设直线l的方程为x=my+1,代入y2=4x,得y2-4my-4=0,利用韦达定理得关系式,再将向量用坐标表示,即可证得;
(ⅱ) 首先可知斜率存在,可设直线l的方程为y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0,根据AB中点横坐标为2,可得方程
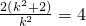 ,进而可求斜率,从而可求AB的长度及l的方程.
,进而可求斜率,从而可求AB的长度及l的方程.点评:本题以抛物线为载体,考查直线与抛物线的位置关系,考查韦达定理的运用,有一定的综合性.

练习册系列答案
相关题目
 (θ为参数)交于A、B两点,试求|PA|+|PB|的最大值.
(θ为参数)交于A、B两点,试求|PA|+|PB|的最大值.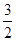 ,点A的坐标为(1+
,点A的坐标为(1+ ),
),  =m·
=m·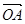 (m为常数),
(m为常数),



 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。