题目内容
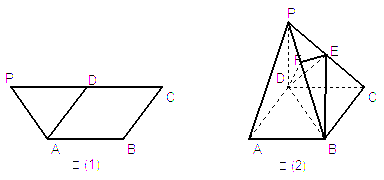
如图示，图（1）四边形ABCP是直角梯形，AB//CP，AB⊥BC，PC=2AB=2BC=4，D是PC的中点，将△PAD沿AD折成如图（2）所示的直二面角P-AD-C，E是PC的中点， 
交PB于点F．(I) 证明 
平面
；(II) 证明
平面EFD；
(III) 求四面体P-EFD的体积
 |
（1）见解析（2）见解析（3）
解析:
(1) 证明：连结AC，AC交BD于O，连结EO．
∵底面ABCD是正方形，∴点O是AC的中点，
在
中，EO是中位线，∴PA // EO，……………………2分
而
平面EDB且
平面EDB，
所以，PA //平面EDB．…………………………………………4分
(2) 证明：∵PD⊥底面ABCD且
底面ABCD，
∴
，
∵PD=DC，可知
是等腰直角三角形，而DE是斜边
PC的 中线，∴
． ①………………………6分
同样由PD⊥底面ABCD，得PD⊥BC．
∵底面ABCD是正方形，有DC⊥BC，∴BC⊥平面PDC．
而
平面PDC，∴
． ②…………………8分
由①和②推得
平面PBC．
而
平面PBC，∴
又且
，所以PB⊥平面EFD．………………………10分
(3) ……………………………………………………………………14分
练习册系列答案
相关题目
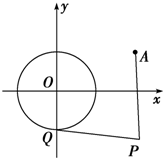已知圆O：x2+y2=1和定点A（2，1），由圆O外一点P（a，b）向圆O引切线PQ，切点为Q，|PQ|=|PA|成立，如图
如图示，在△ABC中，若A，B两点坐标分别为（2，0），（-3，4）点C在AB上，且OC平分∠BOA．
的椭圆
恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k1，k2，若2k1＋k2＝3k，求抛物线C1和椭圆C2的方程．
