题目内容
如图所示,已知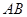 为圆
为圆 的直径,点
的直径,点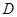 为线段
为线段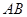 上一点,且
上一点,且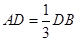 ,点
,点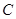 为圆
为圆 上一点,且
上一点,且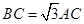 .点
.点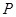 在圆
在圆 所在平面上的正投影为点
所在平面上的正投影为点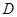 ,
,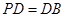 .
.

(1)求证: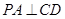 ;
;
(2)求二面角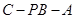 的余弦值.
的余弦值.
【答案】
(1)详见解析;(2)
【解析】
试题分析:(1)要证 ,需先证
,需先证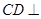 平面
平面 ,由于
,由于 平面
平面 易证,故有
易证,故有 ,又因为
,又因为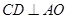 ,则证得
,则证得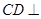 平面
平面 ;(2)综合法是先找到二面角的一个平面角
;(2)综合法是先找到二面角的一个平面角 ,不过必须根据平面角的定义证明,然后在
,不过必须根据平面角的定义证明,然后在 中解出
中解出 的三角函数值.
的三角函数值.
试题解析:(1)连接 ,由
,由 知,点
知,点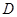 为
为 的中点,
的中点,
又∵ 为圆
为圆 的直径,∴
的直径,∴ ,
,
由 知,
知,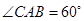 ,
,
∴ 为等边三角形,从而
为等边三角形,从而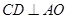 . 3分
. 3分
∵点 在圆
在圆 所在平面上的正投影为点
所在平面上的正投影为点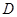 ,
,
∴ 平面
平面 ,又
,又 平面
平面 ,
,
∴ , 5分
, 5分
由 得,
得,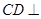 平面
平面 ,
,
又 平面
平面 ,
,
∴ . 6分
. 6分

(2)(综合法)过点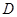 作
作 ,垂足为
,垂足为 ,连接
,连接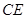 .
7分
.
7分
由(1)知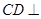 平面
平面 ,又
,又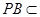 平面
平面 ,
,
∴ ,又
,又 ,
,
∴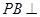 平面
平面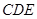 ,又
,又 平面
平面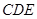 ,∴
,∴ , 9分
, 9分
∴ 为二面角
为二面角 的平面角. 10分
的平面角. 10分
由(Ⅰ)可知 ,
, ,
,
∴ ,则
,则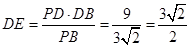 ,
,
∴在 中,
中, ,
,
∴ ,即二面角
,即二面角 的余弦值为
的余弦值为 . 14分
. 14分
考点:1、线线垂直和线面垂直的证明,2、二面角的计算.

练习册系列答案
相关题目
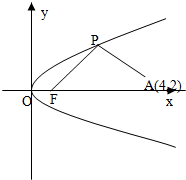 如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.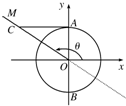 如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?
如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么? 如图所示,已知椭圆C的离心率为
如图所示,已知椭圆C的离心率为 是圆
是圆 的直径,
的直径, 是弦,
是弦, ,垂足为
,垂足为 ,
, 。
。
 与圆
与圆 。
。