题目内容
用一个不平行于底面的平面去截圆锥,在圆锥内作大小两个球分别与圆锥和截面相切.证明截面与两个球的切点恰是椭圆的两个焦点.
证明:
设两个球与平面π的切点分别为F1、F2,与圆锥相切于圆S1、S2,在截口的曲线上任取一点P,连结PF1、PF2,过P作母线交S1于Q1,S2于Q2.
于是PF1和PQ1是从P到上方球的两条切线,因此PF1=PQ1.
同理,PF2=PQ2.
∴PF1+PF2=PQ1+PQ2=Q1Q2.
由正圆锥的对称性,Q1Q2的长度等于两圆S1、S2所在平行平面间的母线段的长度,与P的位置无关.
∴截口椭圆的焦点是F1、F2,即截面与两个球的切点恰是椭圆的两个焦点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的圆柱,截得如图几何体,若截面椭圆的长轴为50
的圆柱,截得如图几何体,若截面椭圆的长轴为50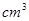 .
.


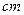 的圆柱,截得如图几何体,若截面椭圆的长轴为50
的圆柱,截得如图几何体,若截面椭圆的长轴为50 .
.