题目内容
如图，用一个不平行于底面的平面
去截圆锥，证明这个平面与圆锥的交线是一个椭圆.
思路点拨：
运用Dandelin双球讨论证明.
证明：如图，在圆锥内部嵌入Dandelin双球，一个位于平面π的上方，一个位于平面π的下方，并且与平面π均相切.
当平面π与底面的夹角β大于圆锥母线与底面的夹角时，平面π与圆锥的交线是一条封闭曲线.
设两个球与平面π的切点分别为F1、F2，与圆锥相切于圆S1、S2，在截口的曲线上任取一点P，连结PF1、PF2，过P作母线交S1于Q1，S2于Q2.
于是PF1和PQ1是从P到上方球的两条切线，因此,PF1=PQ1，同理，PF2=PQ2.
∴PF1+PF2=PQ1+PQ2=Q1Q2.
由正圆锥的对称性，Q1Q2的长度等于两圆S1、S2所在平行平面间的母线段的长度，与P的位置无关.
由此我们可以断定截口的曲线是以F1、F2为焦点的椭圆.
练习册系列答案
阅读快车系列答案
相关题目
，在抛物线上任意画一个点
，度量点
，如图．
时，
，试求抛物线
的方程；
，焦点为
，构造直线
交抛物线
，构造直线
、
分别交准线于
、
两点，构造直线
、
．经观察得：沿着抛物线
.请你证明这一结论． 
”，其余条件不变，发现“
的圆柱，截得如图几何体，若截面椭圆的长轴为50
．
的圆柱，截得如图几何体，若截面椭圆的长轴为50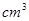
．
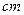的圆柱，截得如图几何体，若截面椭圆的长轴为50
．