题目内容
(理)已知 和
和 ,点T(x,y)满足
,点T(x,y)满足 ,O为直角坐标原点,
,O为直角坐标原点,(1)求点T的轨迹方程Γ;
(2)任意一条不过原点的直线L与轨迹方程Γ相交于点P,Q两点,三条直线OP,OQ,PQ的斜率分别是kOP、kOQ、kPQ,
kPQ2=kOP•kOQ,求kPQ.
【答案】分析:(1)由于点T(x,y)满足
 ,故轨迹是以F1,F2为焦点的椭圆,从而可求轨迹方程;
,故轨迹是以F1,F2为焦点的椭圆,从而可求轨迹方程;
(2)将执行方程与椭圆方程联立,利用斜率公式,结合韦达定理即可证明.
解答:解:(1)由题意,点T的轨迹是以F1,F2为焦点的椭圆,且
从而所求轨迹方程为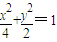 (6分)
(6分)
(2)设直线L的方程:y=kx+t(t≠0)(7分) 消去y得:(1+2k2)x2+4ktx+2t2-4=0,(9分)
消去y得:(1+2k2)x2+4ktx+2t2-4=0,(9分) (10分)
(10分)
消去x得:(1+2k2)y2-2yt+t2-4k2=0, (12分)
(12分)
∴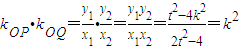 ,(14分)∴
,(14分)∴ ∴
∴ (16分)
(16分)
点评:本题的考点是椭圆的标准方程,主要考查椭圆的定义,考查直线与曲线的位置关系,考查斜率公式,由较强的综合性.

 ,故轨迹是以F1,F2为焦点的椭圆,从而可求轨迹方程;
,故轨迹是以F1,F2为焦点的椭圆,从而可求轨迹方程;(2)将执行方程与椭圆方程联立,利用斜率公式,结合韦达定理即可证明.
解答:解:(1)由题意,点T的轨迹是以F1,F2为焦点的椭圆,且

从而所求轨迹方程为
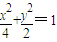 (6分)
(6分)(2)设直线L的方程:y=kx+t(t≠0)(7分)
 消去y得:(1+2k2)x2+4ktx+2t2-4=0,(9分)
消去y得:(1+2k2)x2+4ktx+2t2-4=0,(9分) (10分)
(10分)消去x得:(1+2k2)y2-2yt+t2-4k2=0,
 (12分)
(12分)∴
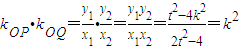 ,(14分)∴
,(14分)∴ ∴
∴ (16分)
(16分)点评:本题的考点是椭圆的标准方程,主要考查椭圆的定义,考查直线与曲线的位置关系,考查斜率公式,由较强的综合性.

练习册系列答案
相关题目
 (理)已知椭圆
(理)已知椭圆 ,且
,且 =1,
=1,
 .
. (文)如图,|AB|=2,O为AB中点,直线
(文)如图,|AB|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与 和
和 ,点T(x,y)满足
,点T(x,y)满足 ,O为直角坐标原点,
,O为直角坐标原点,