题目内容
直线l过点P(-2,3)且与x轴、y轴分别交于A、B两点,若P恰为线段AB的中点,则直线l的方程为__________.
3x-2y+12=0
[解析] 解法一:由题意知直线l的斜率k存在,设直线方程为y-3=k(x+2) (k≠0),即kx-y+2k+3=0,
令x=0,得y=2k+3;令y=0,得x=-![]() -2,
-2,
∴A(-![]() -2,0),B(0,2k+3),
-2,0),B(0,2k+3),
∵AB中点为(-2,3),
∴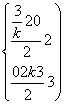 ,得k=
,得k=![]() .
.
∴直线l方程为y-3=![]() (x+2),
(x+2),
即直线l方程为3x-2y+12=0.
解法二:设A(a,0),B(0,b),
∵P为A、B的中点,∴![]() =-2,
=-2,![]() =3,
=3,
∴a=-4,b=6,
∴直线l的方程为![]() +
+![]() =1,即3x-2y+12=0.
=1,即3x-2y+12=0.

练习册系列答案
相关题目
斜率为k的直线l过点P(
,0)且与圆C:x2+y2=1存在公共点,则k2≤
的概率为( )
| 2 |
| 4 |
| 9 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|