题目内容
双曲线H的中心为原点O,离心率e=![]() ,过H上一点P的直线l交H的两渐近线于点P1、P2,已知
,过H上一点P的直线l交H的两渐近线于点P1、P2,已知![]() =2,
=2,
△P1OP2的面积S=![]() .建立适当的坐标系,求H的方程.
.建立适当的坐标系,求H的方程.
解:选坐标系,使H的方程为![]() =1,e=
=1,e=![]() =
=![]() .
.
设a=2m,c=![]() m,b=3m
m,b=3m![]() H:
H:![]() =1.
=1.
渐近线:![]() =0,
=0,
即y=±![]() x,k=tanα=
x,k=tanα=![]() .
.
设P1(x1,![]() x1)、P2(x2,-
x1)、P2(x2,-![]() x2),又P1P=2PP2,
x2),又P1P=2PP2,
分点P(![]() )在H上
)在H上![]() =1,x1·x2=
=1,x1·x2=![]() m2,
m2,
![]() =
=![]() |OP1||OP2|sin2α=
|OP1||OP2|sin2α=![]() ·
·![]() ·|x1|·
·|x1|·![]() |x2|·
|x2|·![]() =
=![]() |x1x2|=
|x1x2|=![]() m2=
m2=![]()
![]() m2=1.
m2=1.
故H的方程为![]() -
-![]() =1.
=1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
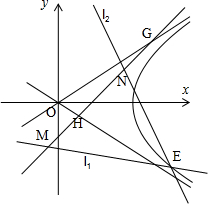
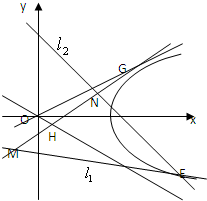
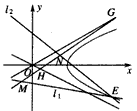
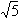 ,0)为右焦点的双曲线C的离心率
,0)为右焦点的双曲线C的离心率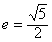 。
。
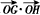 的值。
的值。 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率 .
.