题目内容
已知函数f（x）=x2-（2+m）x+m-1．（1）若函数
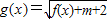定义域为R，求m的取值范围；（2）若不等式f（x）＞0对于|m|≤1恒成立，求x的取值范围．
【答案】分析：（1）根据函数的定义域为R可得x2-（m+2）x+2m+1≥0恒成立，从而有△=（m+2）2-4（2m+1）≤0，故可求m的取值范围；
（2）变换主元，构造以m为变量的函数h（m）=（1-x）m+x2-2x-1＞0，从而转换为h（m）＞0在m∈[-1，1]恒成立，故可求．
解答：解：（1）
，由题意x2-（m+2）x+2m+1≥0恒成立
所以△=（m+2）2-4（2m+1）≤0，则m的取值范围是[0，4]
（2）f（x）=x2-（2+m）x+m-1
令h（m）=（1-x）m+x2-2x-1＞0∵h（m）＞0在m∈[-1，1]恒成立，
∴
∴x＜-1或x＞3
∴x的取值范围是（-∞，-1）∪（3，+∞）
点评：本题以函数为载体，考查恒成立问题，关键是利用判别式求解，同时考查学生分析解决问题的能力．
（2）变换主元，构造以m为变量的函数h（m）=（1-x）m+x2-2x-1＞0，从而转换为h（m）＞0在m∈[-1，1]恒成立，故可求．
解答：解：（1）
，由题意x2-（m+2）x+2m+1≥0恒成立所以△=（m+2）2-4（2m+1）≤0，则m的取值范围是[0，4]
（2）f（x）=x2-（2+m）x+m-1
令h（m）=（1-x）m+x2-2x-1＞0∵h（m）＞0在m∈[-1，1]恒成立，
∴
∴x＜-1或x＞3
∴x的取值范围是（-∞，-1）∪（3，+∞）
点评：本题以函数为载体，考查恒成立问题，关键是利用判别式求解，同时考查学生分析解决问题的能力．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|