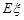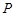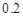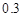题目内容
某运动员射击一次所得环数X的分布列如下:X | 0~6 | 7 | 8 | 9 | 10 |
Y | 0 | 0.2 | 0.3 | 0.3 | 0.2 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为ξ.
(1)求该运动员两次都命中7环的概率;
(2)求ξ的分布列.
思路分析:关键是求出随机变量的取值,这也是近几年高考试题的一个趋势,不给出随机变量的取值,由考生自己给出.
解L1)该运动员两次都命中7环的概率为P(7)=0.2×0.2=0.04.
(2)ξ的可能取值为7、8、9、10,
P(ξ=7)=0.04;P(ξ=8)=2×0.2×0.3+0.32=0.21;
P(ξ=9)=2×0.2×0.3+2×0.3×0.3+0.32=0.39;
P(ξ=10)=2×0.2×0.2+2×0.3×0.2+2×0.3×0.2+0.22=0.36.
ξ的分布列为
ξ | 7 | 8 | 9 | 10 |
P | 0.04 | 0.21 | 0.39 | 0.36 |

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
(06年广东卷)(12分)
某运动员射击一次所得环数X的分布列如下:
X | 0-6 | 7 | 8 | 9 | 10 |
Y | 0 | 0.2 | 0.3 | 0.3 | 0.2 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(Ⅰ)求该运动员两次都命中7环的概率;
(Ⅱ)求![]() 分布列;
分布列;
(Ⅲ) 求![]() 的数学期望.
的数学期望.
(10分)某运动员射击一次所得环数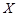 的分布如下:
的分布如下:
|
|
0~6 |
7 |
8 |
9 |
10 |
|
|
0 |
|
|
|
|
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为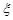 .
.
(I)求该运动员两次都命中7环的概率
(II)求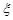 的分布列
的分布列
(III)求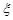 的数学期望
的数学期望