题目内容

△ABC中，若c=
a2+b2+ab
，则角C的度数是（　　）
A．60°B．120°C．60°或120°D．45°
∵△ABC中，c=
a2+b2+ab
，即 a2+b2-c2=-ab，
由余弦定理可得 cosC=
a2+b2-c2
2ab
=-
1
2
，
又 0°＜C＜180°，
∴C=120°，
故选B．
练习册系列答案
相关题目
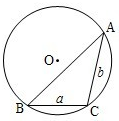精英家教网通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．
（1）如图所示，在以O为圆心，半径为2的⊙O中，BC和BA是⊙O的弦，其中BC=2，∠ABC=45°，求弦AB的长；
（2）在△ABC中，若∠C是钝角，求证：a2+b2＜4R2；
（3）给定三个正实数a、b、R，其中b≤a，问：a、b、R满足怎样的关系时，以a、b为边长，R为外接圆半径的△ABC不存在，存在一个或两个（全等的三角形算作同一个）？在△ABC存在的情况下，用a、b、R表示c．
2、“△ABC中，若∠C=90°，则∠A、∠B都是锐角”的否命题为（　　）
在△ABC中，若角A=60°，b=2，c=1，则边a=
3
3
．
已知函数f（x）=2sinωx+cos（ωx+
π
6
）-sin（ωx-
π
3
）-1（其中ω＞0，x∈R）的最小正周期为4π．
（Ⅰ）求f（x）的最大值和最小值及相应的x的值；
（Ⅱ）在△ABC中，若角A、B、C所对边分别为a、b、c，且f（B）=1，b=3
3
，a+c=3
6
，求sinAsinC的值．
△ABC中，若c=
a2+b2+ab
，则角C的度数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网