题目内容
已知A,B,C均在椭圆M:
+y2=1(a>1)上,直线AB、AC分别过椭圆的左右焦点F1、F2,当
•
=0时,有9
•
=
2.
(Ⅰ)求椭圆M的方程;
(Ⅱ)设是椭圆M上的任一点,EF为圆N:x2+(y-2)2=1的任一条直径,求
•
的最大值.
| x2 |
| a2 |
| AC |
| F1F2 |
| AF1 |
| AF2 |
| AF1 |
(Ⅰ)求椭圆M的方程;
(Ⅱ)设是椭圆M上的任一点,EF为圆N:x2+(y-2)2=1的任一条直径,求
| PE |
| PF |
(Ⅰ)因为
•
=0,所以有
⊥
所以△AF1F2为直角三角形;
∴|
|cos∠F1AF2=|
|
则有9
•
=9|
||
|cos∠F1AF2=9|
|2=
2=|
|2
所以,|
|=3|
|
又|
|+|
|=2a,
∴|
|=
,|
|=
在△AF1F2中有|
|2=|
|2+|
|2
即(
)2=(
)2+4(a2-1),解得a2=2
所求椭圆M方程为
+y2=1
(Ⅱ)由题意可知N(0,2),E,F关于点N对称,
设E(x0,y0),则F(-x0,4-y0)有x02+(y0-2)2=1,
∴
•
=x2-x02+4y0-4y-y02+y2=x2+2y2-(x02+(y0-2)2)-y2+4-4y=-(y+2)2+9
P是椭圆M上的任一点,y∈[-1,1],
所以当y=-1时,
•
的最大值为8.
| AC |
| F1F2 |
| AC |
| F1F2 |
所以△AF1F2为直角三角形;
∴|
| AF1 |
| AF2 |
则有9
| AF1 |
| AF2 |
| AF1 |
| AF2 |
| AF2 |
| AF1 |
| AF1 |
所以,|
| AF1 |
| AF2 |
又|
| AF1 |
| AF2 |
∴|
| AF1 |
| 3a |
| 2 |
| AF2 |
| a |
| 2 |
在△AF1F2中有|
| AF1 |
| AF2 |
| F1F 2 |
即(
| 3a |
| 2 |
| a |
| 2 |
所求椭圆M方程为
| x2 |
| 2 |
(Ⅱ)由题意可知N(0,2),E,F关于点N对称,
设E(x0,y0),则F(-x0,4-y0)有x02+(y0-2)2=1,
∴
| PE |
| PF |
P是椭圆M上的任一点,y∈[-1,1],
所以当y=-1时,
| PE |
| PF |

练习册系列答案
相关题目
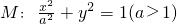 上,直线AB、AC分别过椭圆的左右焦点F1、F2,当
上,直线AB、AC分别过椭圆的左右焦点F1、F2,当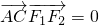 时,有
时,有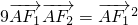 .
. 的最大值.
的最大值.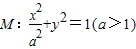 上,直线AB、AC分别过椭圆的左右焦点F1、F2,当
上,直线AB、AC分别过椭圆的左右焦点F1、F2,当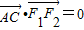 时,有
时,有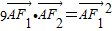 .
.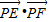 的最大值.
的最大值.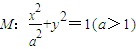 上,直线AB、AC分别过椭圆的左右焦点F1、F2,当
上,直线AB、AC分别过椭圆的左右焦点F1、F2,当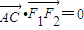 时,有
时,有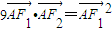 .
.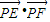 的最大值.
的最大值.