题目内容
已知抛物线 的焦点为
的焦点为 ,点
,点 关于坐标原点对称,以
关于坐标原点对称,以 为焦点的椭圆
为焦点的椭圆 ,过点
,过点
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设 ,过点
,过点 作直线
作直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ,若
,若 ,求
,求 的最小值。
的最小值。
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ)根据题意抛物线的焦点为 ,所以椭圆中
,所以椭圆中 ,再将点
,再将点 代入椭圆方程利用
代入椭圆方程利用 ,求得
,求得 的值,进而求出椭圆的方程;(Ⅱ)根据题意直线
的值,进而求出椭圆的方程;(Ⅱ)根据题意直线 的斜率一定不为
的斜率一定不为 ,设直线
,设直线 的方程为:
的方程为: 联立(Ⅰ)得到的椭圆方程,根据韦达定理得到:
联立(Ⅰ)得到的椭圆方程,根据韦达定理得到: 的值,利用
的值,利用 求得
求得 的取值范围,进而得到
的取值范围,进而得到 的最小值.
的最小值.
试题解析:(Ⅰ)易知 ,椭圆方程为
,椭圆方程为 (5分)
(5分)
(Ⅱ)由题意可设 ,由
,由 (6分)
(6分)
设
将 得
得 (8分)
(8分)
由 得
得 ,
, (9分)
(9分)
 ,
,

 (11分)
(11分)
令
 的最小值是
的最小值是 . (13分)
. (13分)
考点:1.椭圆的方程;2.韦达定理;3.二次函数.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 中,
中, 分别为
分别为 所对的边,若函数
所对的边,若函数 有极值点,则
有极值点,则 的范围是( )
的范围是( ) B.
B. C.
C. D.
D.
 均为锐角,且
均为锐角,且

 C.
C. D.
D.
 的图象经过点
的图象经过点 ,则
,则 。
。 中,公比
中,公比 ,前
,前 项和为
项和为 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,对
,对 的任意非空子集
的任意非空子集 ,定义
,定义 中的最大元素,当
中的最大元素,当 的和为
的和为 ,则①
,则① ;②
;② 。
。 和
和 是计算机在区间
是计算机在区间 上产生的随机数,那么函数
上产生的随机数,那么函数 的值域为
的值域为 (实数集)的概率为( )
(实数集)的概率为( ) B.
B. C.
C. D.
D.
 的顶点都在半径为2的球
的顶点都在半径为2的球 的球面上,且
的球面上,且 ,
, ,过点
,过点 作
作 垂直于平面
垂直于平面 ,交球
,交球 ,则棱锥
,则棱锥 的体积为 .
的体积为 .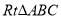 (
(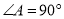 )的外接圆为圆
)的外接圆为圆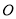 ,过
,过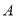 的切线
的切线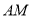 交
交 于点
于点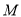 ,过
,过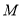 作直线交
作直线交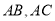 于点
于点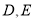 ,且
,且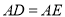

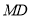 平分角
平分角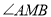 ;
;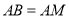 ,求
,求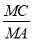 的值.
的值.