题目内容

椭圆ax2+by2=1与直线x+y=1相交于A、B两点；若|AB|=2，且AB的中点C与椭圆中心连线的斜率为，求实数a、b的值.

分析：联立方程组，利用根与系数的关系及弦长公式求解.

解：设椭圆与直线交于A（x1,y1）,B(x2,y2)两点，则由a可得（a+b）x2-2bx+b-1=0.所以x1+x2=,x1x2=,所以|AB|=·|x2-x1|= =2,得（a+b）2=a+b-ab.①

又因为kOC=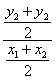=-1==,所以a=b.②

把②代入①，得b=,a=.

点拨：本题设出直线与椭圆的交点，而不求出交点的坐标.

练习册系列答案
相关题目
设椭圆ax2+by2=1与直线x+y-1=0相交于A、B两点，点C是AB的中点，若|AB|=2
2
，OC的斜率为
2
2
，求椭圆的方程．
若椭圆ax2+by2=1与直线x+y=1交于A、B两点，M为AB的中点，直线OM（O为原点）的斜率为
2
2
，且OA⊥OB，求椭圆的方程．
（理）椭圆ax2+by2=1与直线y=-x+1交于A、B两点，过原点与线段AB中点的直线斜率为
2
2
，则
a
b
=
 
．
椭圆ax2+by2=1与直线y=1-2x相交于A、B两点，过原点与线段AB中点的直线的斜率为
3
2
，则
a
b
的值为（　　）
椭圆ax2+by2=1与直线x+y-1=0相交于A，B两点，C是AB的中点，若|AB|=2
2
，OC的斜率为
2
2
，求椭圆的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网