题目内容
已知：g（x）=
|
| 1 |
| 3 |
分析：先求出g（-
）=e-
＞0，则由题意可得 g（g（-
））=g（ e-
）=lne-
=-
．
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答：解：∵g（x）=
，则 g（-
）=e-
＞0，
∴则g（g（-
））=g（ e-
）=lne-
=-
，
故答案为：-
．
|
| 1 |
| 3 |
| 1 |
| 3 |
∴则g（g（-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为：-
| 1 |
| 3 |
点评：本题考查利用分段函数求函数的值，求出g（-
）=e-
＞0，是解题的关键．
| 1 |
| 3 |
| 1 |
| 3 |
练习册系列答案
相关题目
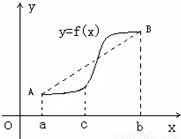
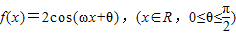，g（x）=ex-x2+2ax-1，（x∈R，a为实数），y=f（x）的图象与y轴交于点
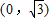，且在该点处切线的斜率为-2．
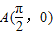，点P是函数y=f（x）图象上一点，Q（x，y）是PA的中点，当
，
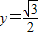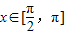时，求x的值；
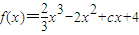，g（x）=ex-e2-x+f（x），
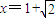处取得极值，试求c的值和f（x）的单调增区间；
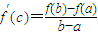，利用这条性质证明：函数y=g（x）图象上任意两点的连线斜率不小于2e-4．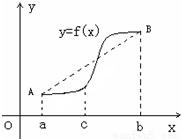
，g（x）=ex-e2-x+f（x），
处取得极值，试求c的值和f（x）的单调增区间；
，利用这条性质证明：函数y=g（x）图象上任意两点的连线斜率不小于2e-4．
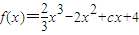，g（x）=ex-e2-x+f（x），
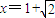处取得极值，试求c的值和f（x）的单调增区间；
，利用这条性质证明：函数y=g（x）图象上任意两点的连线斜率不小于2e-4．