题目内容
已知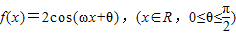 ,g(x)=ex-x2+2ax-1,(x∈R,a为实数),y=f(x)的图象与y轴交于点
,g(x)=ex-x2+2ax-1,(x∈R,a为实数),y=f(x)的图象与y轴交于点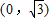 ,且在该点处切线的斜率为-2.
,且在该点处切线的斜率为-2.(I)若点
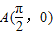 ,点P是函数y=f(x)图象上一点,Q(x,y)是PA的中点,当
,点P是函数y=f(x)图象上一点,Q(x,y)是PA的中点,当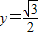 ,
,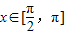 时,求x的值;
时,求x的值;(II)当a>1+ln2时,试问:是否存在曲线y=f(x)与y=g(x)的公切线?并证明你的结论.
【答案】分析:(I)根据在该点 处切线的斜率为-2建立等式关系可求出ω、θ从而求出f(x),利用中点坐标公式建立等式关系,即可求出x的值;
处切线的斜率为-2建立等式关系可求出ω、θ从而求出f(x),利用中点坐标公式建立等式关系,即可求出x的值;
(II)先求出曲线f(x)的切线斜率的取值范围,然后求出曲线y=g(x)的切线斜率的取值范围,看其是否有交集,从而判定是否存在曲线y=f(x)与y=g(x)的公切线.
解答:解:(I)由题意可知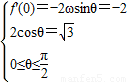 可得:
可得: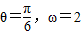
即
设P点坐标为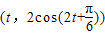 ,已知
,已知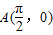
所以Q(x,y)满足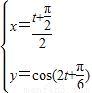 又由
又由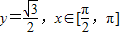 得到t=π或
得到t=π或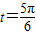
所以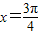 或
或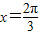
(II)因为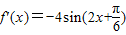 所以曲线f(x)的切线斜率k1∈[-4,4]
所以曲线f(x)的切线斜率k1∈[-4,4]
又g′(x)=ex-2x+2a
∴g″(x)=ex-2
∴令g″(x)=0可得x=ln2处g′(x)取到最小值g′(ln2)=eln2-2ln2+2a>2-2ln2+2+2ln2=4
所以曲线y=g(x)的切线斜率k2>4,故不存在两曲线的共切线.
点评:本题主要考查了利用导数研究在某点处的切线,以及导数的几何意义和公切线问题,属于中档题.
 处切线的斜率为-2建立等式关系可求出ω、θ从而求出f(x),利用中点坐标公式建立等式关系,即可求出x的值;
处切线的斜率为-2建立等式关系可求出ω、θ从而求出f(x),利用中点坐标公式建立等式关系,即可求出x的值;(II)先求出曲线f(x)的切线斜率的取值范围,然后求出曲线y=g(x)的切线斜率的取值范围,看其是否有交集,从而判定是否存在曲线y=f(x)与y=g(x)的公切线.
解答:解:(I)由题意可知
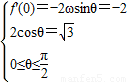 可得:
可得: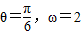
即

设P点坐标为
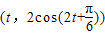 ,已知
,已知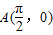
所以Q(x,y)满足
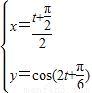 又由
又由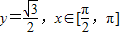 得到t=π或
得到t=π或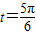
所以
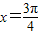 或
或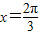
(II)因为
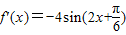 所以曲线f(x)的切线斜率k1∈[-4,4]
所以曲线f(x)的切线斜率k1∈[-4,4]又g′(x)=ex-2x+2a
∴g″(x)=ex-2
∴令g″(x)=0可得x=ln2处g′(x)取到最小值g′(ln2)=eln2-2ln2+2a>2-2ln2+2+2ln2=4
所以曲线y=g(x)的切线斜率k2>4,故不存在两曲线的共切线.
点评:本题主要考查了利用导数研究在某点处的切线,以及导数的几何意义和公切线问题,属于中档题.

练习册系列答案
相关题目
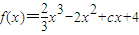 ,g(x)=ex-e2-x+f(x),
,g(x)=ex-e2-x+f(x),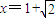 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;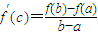 ,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.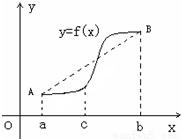
 ,g(x)=ex-e2-x+f(x),
,g(x)=ex-e2-x+f(x), 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间; ,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
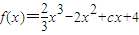 ,g(x)=ex-e2-x+f(x),
,g(x)=ex-e2-x+f(x),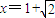 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间; ,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
,利用这条性质证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.