题目内容
定义域为R的函数 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
A
解析试题分析:设 ,则
,则 ,则
,则 ,又
,又 ,∴
,∴ ,∴当
,∴当 时,取到最小值为
时,取到最小值为 .
.
考点:1、函数的解析式;2、二次函数的最值.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
定义: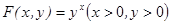 ,已知数列
,已知数列 满足:
满足:
 ,若对任意正整数
,若对任意正整数 ,都有
,都有
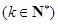 成立,则
成立,则 的值为( )
的值为( )
A. | B. | C.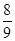 | D. |
给出下列函数:
① ;②
;② ;③
;③ ;④
;④ .
.
则它们共同具有的性质是( )
| A.周期性 | B.偶函数 | C.奇函数 | D.无最大值 |
已知圆 及以下3个函数:①
及以下3个函数:① ;②
;② ;③
;③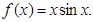 其中图像能等分圆
其中图像能等分圆 面积的函数有
面积的函数有
A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
已知定义域为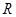 的奇函数
的奇函数 .当
.当 时,
时,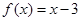 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
下列函数中,既是偶函数,又是在区间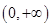 上单调递减的函数是( )
上单调递减的函数是( )
A. | B.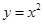 | C. | D. |
已知函数 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.若 ,则 ,则 恒成立 恒成立 |
B.若 恒成立,则 恒成立,则 |
C.若 ,则关于 ,则关于 的方程 的方程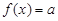 有解 有解 |
D.若关于 的方程 的方程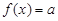 有解,则 有解,则 |
已知 ,
, ,则函数
,则函数 的图象必定不经过( )
的图象必定不经过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
 的图像可能是( )
的图像可能是( )