Question

求证：两两平行的三条直线如果都与另一条直线相交，那么这四条直线共面．

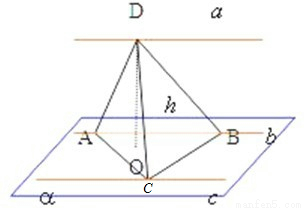
已知a∥b∥c，l∩a＝A，l∩b＝B，l∩c＝C．

求证：直线a、b、c和l共面．

Answer 1

答案：
解析：

如图所示 　　∵a∥b， 　　由推论3可知直线a与b确定一个平面设为α， 　　∵l∩a＝A，l∩b＝B，∴A∈a，B∈b． 　　则A∈α，B∈α， 　　而A∈l，B∈l，∴由公理1可知：lα． 　　∵b∥c， 　　由推论3可知直线b与c确定一个平面，设为β， 　　同理可知lβ． 　　∵平面α和平面β都包含直线b与l，且l∩b＝B， 　　∴由推论2可知：经过两条相交直线，有且只有一个平面， 　　∴平面α与平面β重合， 　　∴直线a、b、c及l共面．