Question

设实数x，y满足x²+（y-1）²=1，则x+y+d≥0恒成立，则d∈（　　）

• A、[

  2

  -1，+∞)
• B、(-∞，

  2

  -1]
• C、[

  2

  +1，+∞)
• D、(-∞，

  2

  +1]

Answer 1

分析：以满足条件的实数（x，y）为坐标的点在以（0，-1）为圆心，半径为1的圆上，再将不等式化为x+y≥-d，转化为x+y的最小值大于或等于-d，找到-d的最大值，即找到d的取值范围．

解答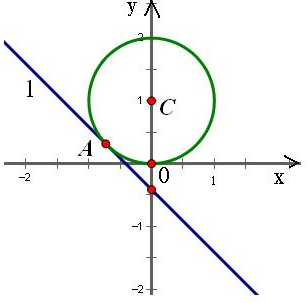：解：由题意，以（x，y）为坐标的点在以（0，-1）为圆心，半径为1的圆上（如图）
不等式x+y+d≥0可化为x+y≥-d，
转化为x+y的最小值大于或等于-d
将直线z=x+y平移，当它在圆C的下方与圆C相切时，z达到最小值
由点C到直线的距离等于1，得

|1-z|

12+12

=1，
所以z的最小值为1-

2

．
故-d≤1-

2

，所以d≥

2

-1．
故选A

点评：本题主要考查直线与圆的位置关系和不等式两个知识点相结合，采用变量分离处理不等式恒成立，属于中档题．