题目内容
若函数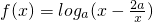
，在x∈（1，2）上单调递减，则a的取值范围是________．
（0，
]
分析：根据函数单调性的性质：增-减=增，可判断内函数u=
，在（1，2）上单调递增，结合复合函数“同增异减”的原则，可得外函数y=logau为减函数，即0＜a＜1，且真数＞0在区是（1，2）上恒成立，由此构造关于a的不等式组，可得答案．
解答：由已知可得a＞0，且a≠1
则函数u=，在（1，2）上单调递增
若函数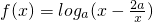，在x∈（1，2）上单调递减，
则外函数y=logau为减函数，即0＜a＜1
且＞0在区是（1，2）上恒成立
即1-2a≥0，解得a≤
综上a的取值范围是（0，]
故答案为：（0，]
点评：本题考查的知识点是函数单调性的性质，对数函数的单调性，对数函数的图象和性质，复合函数的单调性，是函数图象和性质的综合应用，难度较大．
]分析：根据函数单调性的性质：增-减=增，可判断内函数u=
，在（1，2）上单调递增，结合复合函数“同增异减”的原则，可得外函数y=logau为减函数，即0＜a＜1，且真数＞0在区是（1，2）上恒成立，由此构造关于a的不等式组，可得答案．解答：由已知可得a＞0，且a≠1
则函数u=
，在（1，2）上单调递增若函数
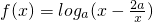，在x∈（1，2）上单调递减，则外函数y=logau为减函数，即0＜a＜1
且
＞0在区是（1，2）上恒成立即1-2a≥0，解得a≤
综上a的取值范围是（0，
]故答案为：（0，
]点评：本题考查的知识点是函数单调性的性质，对数函数的单调性，对数函数的图象和性质，复合函数的单调性，是函数图象和性质的综合应用，难度较大．
练习册系列答案
阅读快车系列答案
相关题目
设函数f（x）=定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界、若函数f（x）=1+a•(
)x+(
)x在[0，+∞）上是以3为上界的有界函数，则实数a的取值范围是（ ）
| 1 |
| 2 |
| 1 |
| 4 |
| A、[-5，0] |
| B、[-4，1] |
| C、[-4，0] |
| D、[-5，1] |