题目内容
已知中心在坐标原点,对称轴为坐标轴的双曲线C的离心率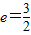 ,一条准线方程为
,一条准线方程为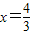 ,则双曲线C的渐近线方程为( )
,则双曲线C的渐近线方程为( )A.
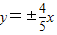
B.
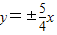
C.
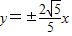
D.
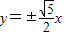
【答案】分析:通过双曲线的准线方程判断双曲线的焦点所在轴,利用离心率与准线方程,求出a,c,然后求出渐近线方程.
解答:解:因为已知中心在坐标原点,对称轴为坐标轴的双曲线C的离心率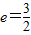 ,一条准线方程为
,一条准线方程为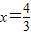 ,
,
则双曲线的焦点在x轴,所以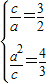 ,所以a=2,c=3,则b=
,所以a=2,c=3,则b=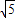 ,
,
所以双曲线的渐近线方程为: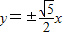 .
.
故选D.
点评:本题考查双曲线的简单性质的应用,判断双曲线的焦点所在轴是解题的关键,考查计算能力.
解答:解:因为已知中心在坐标原点,对称轴为坐标轴的双曲线C的离心率
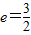 ,一条准线方程为
,一条准线方程为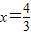 ,
,则双曲线的焦点在x轴,所以
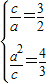 ,所以a=2,c=3,则b=
,所以a=2,c=3,则b=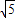 ,
,所以双曲线的渐近线方程为:
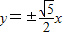 .
.故选D.
点评:本题考查双曲线的简单性质的应用,判断双曲线的焦点所在轴是解题的关键,考查计算能力.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 (2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率
(2013•丽水一模)已知中心在坐标原点,焦点在x轴上的椭圆过点P(2,3),且它的离心率