题目内容
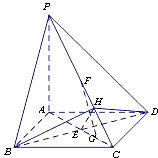
【题目】如图,在底面是正方形的四棱锥P﹣ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 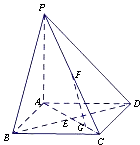
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(3)当二面角B﹣PC﹣D的大小为 ![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
【答案】
(1)证明:∵PA⊥面ABCD,四边形ABCD是正方形,其对角线BD,AC交于点E,
∴PA⊥BD,AC⊥BD,
∴BD⊥平面PAC,
∵FG平面PAC,
∴BD⊥FG
或用向量方法:
解:以A为原点,AB,AD,AP所在的直线分别为x,y,z轴建立空间直角坐标系如图所示,设正方形ABCD的边长为1,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,a)(a>0),
E( ![]() ),F(
),F( ![]() ),G(m,m,0)(0<m<
),G(m,m,0)(0<m< ![]() )
)
![]() =(﹣1,1,0),
=(﹣1,1,0), ![]() =(
=( ![]() ),
), ![]() ×
× ![]() =﹣m+
=﹣m+ ![]() +m﹣
+m﹣ ![]() +0=0,
+0=0,
∴BD⊥FG
(2)解:当G为EC中点,即AG= ![]() AC时,FG∥平面PBD,
AC时,FG∥平面PBD,
理由如下:
连接PE,由F为PC中点,G为EC中点,知FG∥PE,
而FG平面PBD,PE平面PBD,
故FG∥平面PBD.
或用向量方法:
要使FG∥平面PBD,只需FG∥EP,而 ![]() =(
=( ![]() ),由
),由 ![]() =
= ![]()
![]() 可得
可得 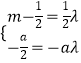 ,
,
解得l=1,m= ![]() ,
,
∴G( ![]() ,
, ![]() ,0),∴
,0),∴ ![]() ,
,
故当AG= ![]() AC时,FG∥平面PBD
AC时,FG∥平面PBD
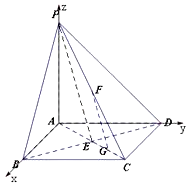
(3)解:作BH⊥PC于H,连接DH,
∵PA⊥面ABCD,四边形ABCD是正方形,
∴PB=PD,
又∵BC=DC,PC=PC,
∴△PCB≌△PCD,
∴DH⊥PC,且DH=BH,
∴∠BHD就是二面角B﹣PC﹣D的平面角,
即∠BHD= ![]() ,
,
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角
连接EH,则EH⊥BD,∠BHE= ![]() ,EH⊥PC,
,EH⊥PC,
∴tan∠BHE= ![]() ,而BE=EC,
,而BE=EC,
∴ ![]() ,∴sin∠PCA=
,∴sin∠PCA= ![]() ,∴tan∠PCA=
,∴tan∠PCA= ![]() ,
,
∴PC与底面ABCD所成角的正切值是 ![]()
或用向量方法:
设平面PBC的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 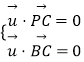 ,而
,而 ![]() ,
, ![]() ,
,
∴ ![]() ,取z=1,得
,取z=1,得 ![]() =(a,0,1),同理可得平面PDC的一个法向量为
=(a,0,1),同理可得平面PDC的一个法向量为 ![]() =(0,a,1),
=(0,a,1),
设 ![]() ,
, ![]() 所成的角为β,则|cosβ|=|cos
所成的角为β,则|cosβ|=|cos ![]() |=
|= ![]() ,即
,即 ![]() =
= ![]() ,∴
,∴ ![]() ,∴a=1
,∴a=1
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角,
∴tan∠PCA= ![]()
【解析】(1)要证:BD⊥FG,先证BD⊥平面PAC即可.(2)确定点G在线段AC上的位置,使FG∥平面PBD,FG∥平面PBD内的一条直线即可.(3)当二面角B﹣PC﹣D的大小为 ![]() 时,求PC与底面ABCD所成角的正切值.只要作出二面角的平面角,解三角形即可求出结果.这三个问题可以利用空间直角坐标系,解答(1)求数量积即可.(2)设才点的坐标,向量共线即可解答.(3)利用向量数量积求解法向量,然后转化求出PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.只要作出二面角的平面角,解三角形即可求出结果.这三个问题可以利用空间直角坐标系,解答(1)求数量积即可.(2)设才点的坐标,向量共线即可解答.(3)利用向量数量积求解法向量,然后转化求出PC与底面ABCD所成角的正切值.
【考点精析】通过灵活运用空间中直线与直线之间的位置关系和平面与平面之间的位置关系,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;两个平面平行没有交点;两个平面相交有一条公共直线即可以解答此题.

 科学实验活动册系列答案
科学实验活动册系列答案