题目内容
设O为坐标原点,F1,F2是椭圆 的左、右焦点,若在椭圆上存在点P满足
的左、右焦点,若在椭圆上存在点P满足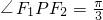 ,且
,且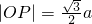 ,则该椭圆的离心率为________.
,则该椭圆的离心率为________.

分析:由于
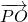 =
= (
( +
+ ),两边平方,再利用余弦定理即可求得该椭圆的离心率.
),两边平方,再利用余弦定理即可求得该椭圆的离心率.解答:令|
 |=m,|
|=m,| |=n,m+n=2a.
|=n,m+n=2a.∵
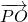 =
= (
( +
+ ),
),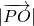 =
= a,
a,∴
 =
= (
( +2
+2 •
• +
+ )
)即
 a2=
a2= (m2+2mncos
(m2+2mncos +n2),
+n2),∴3a2=m2+n2+mn=(m+n)2-mn=4a2-mn,
∴a2=mn.
在△PF1F2中,由余弦定理得:
 =m2+n2-2mn×
=m2+n2-2mn× =(m+n)2-3mn,
=(m+n)2-3mn,即4c2=4a2-3mn=4a2-3a2=a2,
∴e=
 =
= .
.故答案为:
 .
.点评:本题考查向量的数量积与余弦定理的综合应用,考查方程思想与运算能力,属于中档题.

练习册系列答案
相关题目
设O为坐标原点,F1,F2是双曲线
-
=1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1PF2=60°,|OP|=
a,则该双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
A、x±
| ||
B、
| ||
C、x±
| ||
D、
|