已知点为坐标原点.动点满足.则点所构成的平面区域的面积是A．12B．16C．32D．64 题目和参考答案——青夏教育精英家教网——

题目内容

已知点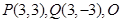为坐标原点，动点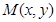满足，则点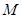所构成的平面区域的面积是（）

A．12

B．16

C．32

D．64

C

解析试题分析：由于点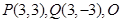为坐标原点，所以设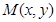.所以.所以.由可得.所以可行域是一个对角线为8的正方形，所以面积为.故选C.
考点：1.向量的数量积.2.线性规划.3.绝对值不等式的解法.

练习册系列答案

金色阳光AB卷系列答案

高分计划一卷通系列答案

单元测评卷精彩考评七年级下数学延边教育出版社系列答案

王朝霞期末真题精编系列答案

各地期末名卷精选系列答案

导与练初中同步练案系列答案

满分夺冠期末测试卷系列答案

优生乐园系列答案

钟书金牌上海新卷系列答案

加分猫汇练系列答案

相关题目

若向量满足且，则( )

已知e₁，e₂是夹角为60°的两个单位向量，若a＝e₁＋e₂，b＝－4e₁＋2e₂，则a与b的夹角为( )

已知、均为单位向量，它们的夹角为，那么（）

若，且与的夹角为，当取得最小值时，实数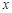的值为（）

已知向量都是单位向量，且，则的值为（）

已知则与的夹角为 ( )

对于向量a，b，定义a×b为向量a，b的向量积，其运算结果为一个向量，且规定a×b的模|a×b|＝|a||b|sin θ(其中θ为向量a与b的夹角)，a×b的方向与向量a，b的方向都垂直，且使得a，b，a×b依次构成右手系．如图所示，在平行六面体ABCD－EFGH中，∠EAB＝∠EAD＝∠BAD＝60°，AB＝AD＝AE＝2，则(×)·＝( )

已知向量a＝(1，2)，b＝(1，0)，c＝(3，4)，若λ为实数，且(b＋λa)⊥c，则λ＝(　　)