题目内容
从原点向圆x2+(y-6)2=4作两条切线,则这两条切线夹角的大小为
- A.

- B.

- C.arccos

- D.arcsin

C
分析:根据AB⊥OB以及圆的方程求出|OA|,|AB|,|AC|,在直角三角形中求出sin∠AOB,然后根据△OAB≌△OAC求出∠BOC,其中∠BOC为∠AOB的两倍
解答: 解:如图,从原点向圆A引两条切线:OB,OC,连接AB,AC
解:如图,从原点向圆A引两条切线:OB,OC,连接AB,AC
∴AB⊥OB,AC⊥OC
∵圆x2+(y-6)2=4
∴|OA|=6,|AB|=|AC|=2
且△OAB≌△OAC
在RT△AOB中:
sin∠AOB=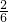 =
= ,
,
∴由△OAB≌△OAC
cos∠BOC=cos2∠AOB=1-2sin2∠AOB=1- =
= ,
,
∴∠BOC=arccos ,
,
故选C.
点评:本题考查2倍角的正弦和余弦公式的利用,涉及到直线与圆相切,三角形相似等内容,属于难题.
分析:根据AB⊥OB以及圆的方程求出|OA|,|AB|,|AC|,在直角三角形中求出sin∠AOB,然后根据△OAB≌△OAC求出∠BOC,其中∠BOC为∠AOB的两倍
解答:
 解:如图,从原点向圆A引两条切线:OB,OC,连接AB,AC
解:如图,从原点向圆A引两条切线:OB,OC,连接AB,AC∴AB⊥OB,AC⊥OC
∵圆x2+(y-6)2=4
∴|OA|=6,|AB|=|AC|=2
且△OAB≌△OAC
在RT△AOB中:
sin∠AOB=
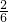 =
= ,
,∴由△OAB≌△OAC
cos∠BOC=cos2∠AOB=1-2sin2∠AOB=1-
 =
= ,
,∴∠BOC=arccos
 ,
,故选C.
点评:本题考查2倍角的正弦和余弦公式的利用,涉及到直线与圆相切,三角形相似等内容,属于难题.

练习册系列答案
相关题目
从原点向圆x2+(y-6)2=4作两条切线,则这两条切线夹角的大小为( )
A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arcsin
|



