题目内容
根据下列条件求直线方程
(1)过点(2,1)且倾斜角为 的直线方程;
的直线方程;
(2)过点(-3,2)且在两坐标轴截距相等的直线方程.
解:(1)由题意可得直线的斜率为tan =
= ,
,
由点斜式方程可得:y-1= (x-2),
(x-2),
化为一般式可得: (4分)
(4分)
(2)若直线过原点,则可设方程为y=kx,
代入点(-3,2),可得k= ,故直线为
,故直线为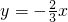 ,
,
化为一般式可得:2x+3y=0;
若直线不过原点,可设方程为 ,
,
代入点(-3,2),可得a=-1,
故所求直线的方程为:x+y+1=0,
故所求直线的方程为:2x+3y=0或x+y+1=0 (每一个方程3分)
分析:(1)由题意可得直线的斜率为 ,由点斜式可写方程,化为一般式即可;(2)注意分直线过原点和不过原点两类,由截距的概念分别求解,即得答案.
,由点斜式可写方程,化为一般式即可;(2)注意分直线过原点和不过原点两类,由截距的概念分别求解,即得答案.
点评:本题考查直线方程的求解,注意最终化为一般式,属基础题.
 =
= ,
,由点斜式方程可得:y-1=
 (x-2),
(x-2),化为一般式可得:
 (4分)
(4分)(2)若直线过原点,则可设方程为y=kx,
代入点(-3,2),可得k=
 ,故直线为
,故直线为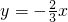 ,
,化为一般式可得:2x+3y=0;
若直线不过原点,可设方程为
 ,
,代入点(-3,2),可得a=-1,
故所求直线的方程为:x+y+1=0,
故所求直线的方程为:2x+3y=0或x+y+1=0 (每一个方程3分)
分析:(1)由题意可得直线的斜率为
 ,由点斜式可写方程,化为一般式即可;(2)注意分直线过原点和不过原点两类,由截距的概念分别求解,即得答案.
,由点斜式可写方程,化为一般式即可;(2)注意分直线过原点和不过原点两类,由截距的概念分别求解,即得答案.点评:本题考查直线方程的求解,注意最终化为一般式,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的直线方程;
的直线方程; 的直线方程;
的直线方程; 的直线方程;
的直线方程;