题目内容
圆C:x2+y2+2x+4y-3=0上到直线 :x+y+1=0的距离为
:x+y+1=0的距离为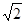 的点共有( )
的点共有( )
 :x+y+1=0的距离为
:x+y+1=0的距离为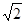 的点共有( )
的点共有( )| A.1个 | B.2个 | C.3个 | D.4个 |
C
试题分析:将圆的方程化为标准方程得:(x+1)2+(y+2)2=8,所以圆心坐标为(-1,-2),半径为2
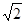 ,所以圆心到直线x+y+1=0的距离d=
,所以圆心到直线x+y+1=0的距离d=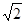 ,则圆上到直线x+y+1=0的距离为
,则圆上到直线x+y+1=0的距离为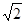 的点共有3个。故选C。
的点共有3个。故选C。点评:熟练运用点到直线的距离公式是解本题的关键。

练习册系列答案
相关题目
 上的点到直线
上的点到直线 距离的最大值是( )
距离的最大值是( ) 
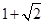


 是圆
是圆 上的动点.
上的动点. 的距离的最小值;
的距离的最小值; 与圆
与圆 相切,且
相切,且 两点,求
两点,求 的面积最小时直线
的面积最小时直线 和
和 为直径端点的圆的方程是
为直径端点的圆的方程是



 中,“直线
中,“直线 ,
, 与曲线
与曲线 相切”的充要条件是 .
相切”的充要条件是 . 过定点
过定点 ,且与直线
,且与直线 相切,椭圆
相切,椭圆 的对称轴为坐标轴,一个焦点为
的对称轴为坐标轴,一个焦点为 ,点
,点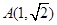 在椭圆
在椭圆 的方程及椭圆
的方程及椭圆 与轨迹
与轨迹 处的切线平行,且直线
处的切线平行,且直线 两点,试求当
两点,试求当 面积取到最大值时直线
面积取到最大值时直线 与圆
与圆 相交于A、B两点,且弦AB的长为2
相交于A、B两点,且弦AB的长为2 ,则
,则 =________.
=________. ,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点.
,△ABC内接于此圆,A点的坐标(3,4),O为坐标原点. ,2),求BC中点D的坐标及直线BC的方程;
,2),求BC中点D的坐标及直线BC的方程; 上的点到直线
上的点到直线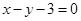 的距离的最大值是( )
的距离的最大值是( )