题目内容
16.若函数f(x)=2|x-1|且f(x)在[m,+∞)上单调递增,则实数m的最小值等于1.分析 先将函数解析式化为分段函数的形式,进而求出函数的单调递增区间,结合已知可得答案.
解答 解:函数f(x)=2|x-1|=$\left\{\begin{array}{l}{2}^{1-x},x<1\\{2}^{x-1},x≥1\end{array}\right.$,
则函数f(x)的单调递增区间为[1,+∞),
若函数f(x)=2|x-1|且f(x)在[m,+∞)上单调递增,
则[m,+∞)⊆[1,+∞),
即m≥1,
即实数m的最小值等于1,
故答案为:1.
点评 本题考查的知识点是分段函数的应用,指数函数的图象和性质,复合函数的单调性,单调性的性质,难度中档.

练习册系列答案
相关题目
6.已知复数z=a+bi(a,b∈R,且ab≠0),若z(1-2i)为实数,则$\frac{b}{a}$=( )
| A. | 2 | B. | -2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
11.已知等差数列{an}的公差d=-2,a1+a4+a7+…+a97=50,那么a3+a6+a9+…+a99的值是( )
| A. | -78 | B. | -82 | C. | -148 | D. | -182 |
8.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y-2≤0}\\{y≤1}\end{array}\right.$,则目标函数z=x+2y的最小值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
5.如图是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是( )
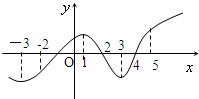
| A. | 在区间(-2,1)上f(x)是增函数 | B. | 当x=4时,f(x)取极大值 | ||
| C. | 在(1,3)上f(x)是减函数 | D. | 在(4,5)上f(x)是增函数 |
6.等差数列{an}中,a1•a2015为方程x2-10x+21=0的两根,则a2+a2014=( )
| A. | 10 | B. | 15 | C. | 20 | D. | 40 |
 已知A={x|log2(x+1)<2},B={x|x-1>0}
已知A={x|log2(x+1)<2},B={x|x-1>0}


