题目内容
4．
已知A={x|log2（x+1）＜2}，B={x|x-1＞0}（Ⅰ）求A∩B和A∪B；
（Ⅱ）若记符号A-B={x|x∈A，且x∉B}，在图中把表示“集合A-B”的部分用阴影涂黑；并求A-B．
分析 先求出关于集合A，B中的x的范围，从而求出A∩B、A∪B、A-B．
解答 解：已知A={x|log2（x+1）＜2}={x|-1＜x＜3}，
B={x|x-1＞0}={x|x＞1}，
（Ⅰ）A∩B=（-1，3）∩（1，+∞）=（1，3），
A∪B=（-1，+∞）；
（Ⅱ）A-B={x|x∈A，且x∉B}=（-1，1]，
如图示：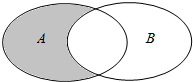
．
点评 本题考查了集合的运算，考查对数函数的性质，是一道基础题．
练习册系列答案
中考解读考点精练系列答案
相关题目
14．设$X～B（5，\frac{1}{3}）$，则P（X≤4）等于 （ ）
| A． | $\frac{10}{243}$ | B． | $\frac{242}{243}$ | C． | $\frac{241}{243}$ | D． | 1 |
19．若存在实数m，n，使得$\frac{1}{e^x}-\frac{a}{x}≥0$的解集为[m，n]，则a的取值范围为（ ）
| A． | $（\frac{1}{e^2}，e）$ | B． | $（0，\frac{1}{e^2}）$ | C． | $（0，\frac{1}{2e}）$ | D． | $（0，\frac{1}{e}）$ |
13．已知集合M={0，1}，集合N={x|x2+x=0），则集合M∪N等于（ ）
| A． | 0 | B． | {0} | C． | ∅ | D． | {-1，0，1} |