题目内容
18.设函数f(x)=sin($\frac{1}{2}$x+φ)(0<φ<$\frac{π}{2}$),y=f(x)图象的一条对称轴是直线x=$\frac{π}{4}$.(1)求φ
(2)求函数f(x)图象的对称中心.
分析 (1)利用x=$\frac{π}{4}$是函数y=f(x)的图象的对称轴,可求得φ=$\frac{3π}{8}$+kπ,又0<ϕ<π,从而可得φ的值;
(2)利用正弦函数的图象和性质,根据$\frac{1}{2}$x+$\frac{3π}{8}$=kπ,k∈Z,可解得对称中心.
解答 解:(1)∵x=$\frac{π}{4}$是函数y=f(x)的图象的对称轴,
∴sin(φ+$\frac{1}{2}$×$\frac{π}{4}$)=±1,
∴φ+$\frac{π}{8}$=k$π+\frac{π}{2}$,k∈Z,
∴φ=kπ+$\frac{3π}{8}$,又0<ϕ<$\frac{π}{2}$,
∴φ=$\frac{3π}{8}$.
(2)由(1)得函数f(x)的解析式为y=sin($\frac{1}{2}$x+$\frac{3π}{8}$),
由$\frac{1}{2}$x+$\frac{3π}{8}$=kπ,k∈Z,可解得对称中心为:(2kπ-$\frac{3π}{4}$,0)
点评 本题考查正弦函数的图象和对称性,求得φ的值是关键,考查了分析、运算、求解能力,属于中档题.

练习册系列答案
相关题目
3.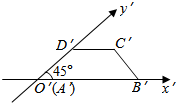 如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )
如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )
 如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )
如图是一个水平放置的直观图,它是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积为( )| A. | 2+$\sqrt{2}$ | B. | $\frac{{1+\sqrt{2}}}{2}$ | C. | $\frac{{2+\sqrt{2}}}{2}$ | D. | 1+$\sqrt{2}$ |