题目内容
已知等差数列的前10项和为310,前20项和是1 220,试写出这个数列的前n项和公式.
思路解析:根据题设条件列出方程组,求出a1和d,代入等差数列前n项和公式即得. 解法一:由题意知 即 故S n=4n+ 解法二:由数列为等差数列,设其前n项和为Sn=pn2+qn, 则有 解得

 解得
解得
![]() ×6=3n2+n.
×6=3n2+n.
![]() 故Sn=3n2+n.
故Sn=3n2+n. 练习册系列答案
练习册系列答案
新编助学读本系列答案
数学课堂与感悟系列答案
单元双测专题期中期末大试卷系列答案
金点考单元同步检测系列答案
素质目标检测系列答案
每课100分系列答案
智慧学习导学练系列答案
学科王同步课时练习系列答案
三维导学案系列答案
单元双测试卷系列答案
相关题目
 的前四项和为10,且
的前四项和为10,且 成等比数列
成等比数列
 ,求数列
,求数列 的前
的前 项和
项和
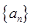 的前四项和为10,且
的前四项和为10,且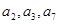 成等比数列
成等比数列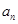
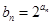 ,求数列
,求数列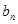 的前
的前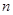 项和
项和 。
。 的前n项和为
的前n项和为 ,若M、N、P三点共线,O为坐标原点,且
,若M、N、P三点共线,O为坐标原点,且 (直线MP不过点O),则S20等于( )
(直线MP不过点O),则S20等于( )