题目内容
一个平面截一个球得到截面面积为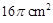 的圆面,球心到这个平面的距离是
的圆面,球心到这个平面的距离是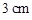 ,则该球的表面积是( )
,则该球的表面积是( )
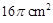 的圆面,球心到这个平面的距离是
的圆面,球心到这个平面的距离是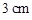 ,则该球的表面积是( )
,则该球的表面积是( )
A.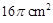 | B. | C.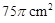 | D.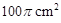 |
D
一个平面截一个球得到截面面积为
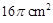 的圆面,圆面的半径为4cm
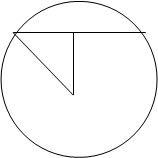
的圆面,圆面的半径为4cm过球心和圆面的圆心的截面,示意图如右图,则勾股定理得球的半径R=5cm
则该球的表面积是
 ,故选择D
,故选择D
练习册系列答案
相关题目
题目内容
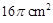 的圆面,球心到这个平面的距离是
的圆面,球心到这个平面的距离是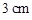 ,则该球的表面积是( )
,则该球的表面积是( )
A.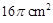 | B. | C.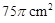 | D.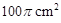 |
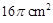 的圆面,圆面的半径为4cm
的圆面,圆面的半径为4cm ,故选择D
,故选择D