题目内容

(Ⅰ)易证 ;令
;令 ,
,
(Ⅱ)假设方程f(x)﹣x=0存在两个实数根α,β(α≠β),
则f(α)﹣α=0,f(β)﹣β=0
不妨设α<β,
根据题意存在数c (α,β)使得等式f(β)﹣f(α)=(β﹣α)f'(c)成立.
(α,β)使得等式f(β)﹣f(α)=(β﹣α)f'(c)成立.
因为f(α)=α,f (β)=β,且α≠β,
(β)=β,且α≠β,
所以f'(c)=1,与已知0<f'(x)<1矛盾,
所以方程f(x)﹣x=0只有一个实数根;
(Ⅲ)当 时,结论显然成立;
时,结论显然成立;
当 ,不妨设
,不妨设 .
.
因为 ,且
,且 所以
所以 为增函数,那么
为增函数,那么 .
.
又因为 ,所以函数
,所以函数 为减函数,
为减函数,
所以 .
.
所以 ,即
,即 .
.
因为 ,所以
,所以 , (1)
, (1)
又因为 ,所以
,所以 , (
, ( 2)
2)
(1) (2)得
(2)得 即
即 .
.
所以
 .
.
综上,对于任意符合条件的 ,
, 总成立
总成立

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为
的三棱锥的四个顶点全部在同一个球面上,则该球的表面积为 (B)
(B) (C)
(C) (D)
(D)
 ,则
,则 .
. R,
R, ”的否定是( )
”的否定是( ) B.不存在
B.不存在 R,
R,  R,
R, 上的偶函数
上的偶函数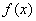 在
在 上为减函数,且
上为减函数,且 ,则满足
,则满足 的
的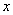 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.
 的解集是___________.
的解集是___________. 表示平面,a、b表示两条不同的直线,给定下列四个命题:①若a∥
表示平面,a、b表示两条不同的直线,给定下列四个命题:①若a∥ 为等差数列,其前
为等差数列,其前 项和为
项和为 .若
.若 ,
, ,
, ,则
,则 .
.