题目内容
函数y=cos4x-sin4x的最小正周期是（ ）A．
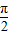
B．π
C．2π
D．4π
【答案】分析：观察题目条件，思路是降幂，先用平方差公式，再逆用二倍角公式，式子变为能判断周期等性质的形式，即y=Asin（ωx+φ）的形式．
解答：解：∵y=cos4x-sin4x
=cos2x-sin2x
=cos2x，
∴T=π，
故选B
点评：对于和式的整理，基本思路是降次、消项和逆用公式，本题就是逆用余弦的二倍角公式．另外还要注意切割化弦，变量代换和角度归一等方法．
解答：解：∵y=cos4x-sin4x
=cos2x-sin2x
=cos2x，
∴T=π，
故选B
点评：对于和式的整理，基本思路是降次、消项和逆用公式，本题就是逆用余弦的二倍角公式．另外还要注意切割化弦，变量代换和角度归一等方法．
练习册系列答案
名校课堂系列答案
相关题目
下列命题正确的是（ ）
| A、函数y=sinx在区间（0，π）内单调递增 | ||||
B、函数y=tanx的图象是关于直线x=
| ||||
| C、函数y=cos4x-sin4x的最小正周期为2π | ||||
D、函数y=cos(x+
|