题目内容
已知函数f(x)=a1x+a2x2+a3x3+…+anxn,n∈N*且a1、a2、a3、……、an构成一个数列{an},满足f(1)=n2.
(1)求数列{an}的通项公式,并求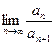 ;
;
(2)证明0<f( )<1.
)<1.
(1)求数列{an}的通项公式,并求
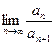 ;
;(2)证明0<f(
 )<1.
)<1.(1)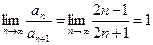 (2)证明略
(2)证明略
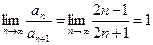 (2)证明略
(2)证明略 (1)解: {an}的前n项和Sn=a1+a2+…+an=f(1)=n2,
由an=Sn–Sn–1=n2–(n–1)2=2n–1(n≥2),又a1=S1=1满足an=2n–1.
故{an}通项公式为an=2n–1(n∈N*)
∴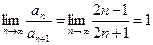
(2)证明: ∵f( )=1·
)=1· +3·
+3·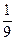 +…+(2n–1)
+…+(2n–1)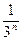 ①
①
∴ f(
f( )=1·
)=1·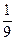 +3·
+3·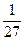 +…+(2n–3)
+…+(2n–3)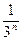 +(2n–1)
+(2n–1)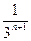 ②
②
①–②得: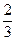 f(
f( )=1·
)=1· +2·
+2·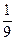 +2·
+2·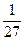 +…+2·
+…+2·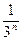 –(2n–1)·
–(2n–1)·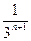
∴f( )=
)=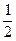 +
+ +
+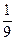 +
+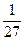 +…+
+…+ –(2n–1)
–(2n–1)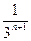 =1–
=1–

∵ (n∈N*)
(n∈N*)
∴0< <1,∴0<1–
<1,∴0<1– <1,即0<f(
<1,即0<f( )<1
)<1
由an=Sn–Sn–1=n2–(n–1)2=2n–1(n≥2),又a1=S1=1满足an=2n–1.
故{an}通项公式为an=2n–1(n∈N*)
∴
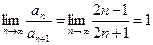
(2)证明: ∵f(
 )=1·
)=1· +3·
+3·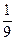 +…+(2n–1)
+…+(2n–1)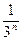 ①
①∴
 f(
f( )=1·
)=1·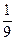 +3·
+3·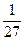 +…+(2n–3)
+…+(2n–3)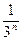 +(2n–1)
+(2n–1)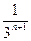 ②
②①–②得:
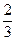 f(
f( )=1·
)=1· +2·
+2·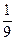 +2·
+2·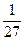 +…+2·
+…+2·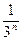 –(2n–1)·
–(2n–1)·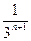
∴f(
 )=
)=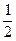 +
+ +
+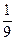 +
+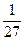 +…+
+…+ –(2n–1)
–(2n–1)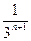 =1–
=1–

∵
 (n∈N*)
(n∈N*)∴0<
 <1,∴0<1–
<1,∴0<1– <1,即0<f(
<1,即0<f( )<1
)<1
练习册系列答案
相关题目
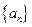 是等差数列.
是等差数列.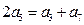 是否成立?
是否成立?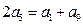 呢?为什么?
呢?为什么?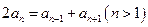 是否成立?据此你能得出什么结论?
是否成立?据此你能得出什么结论?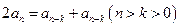 是否成立?你又能得出什么结论?
是否成立?你又能得出什么结论?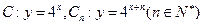 ,从
,从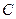 上的点
上的点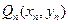 作
作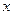 轴的垂线,交
轴的垂线,交 于点
于点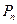 ,再从点
,再从点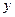 轴的垂线,交
轴的垂线,交 ,设
,设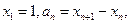

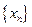 的通项公式;
的通项公式; ,数列
,数列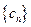 的前
的前 项和为
项和为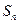 ,试比较
,试比较 的大小
的大小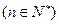 ;
;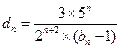 ,数列
,数列 的前
的前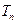 ,试证明:
,试证明: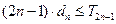

 满足
满足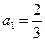 ,
,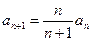 ,求
,求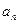 。
。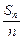 -1)为坐标的点Pn(n=1,2,…)都落在同一条直线上,并写出此直线的方程.
-1)为坐标的点Pn(n=1,2,…)都落在同一条直线上,并写出此直线的方程.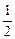 ,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1、P2、P3都落在圆C外时,r的取值范围.
,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1、P2、P3都落在圆C外时,r的取值范围.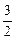 (an-1),数列{bn}的通项公式为bn=4n+3;
(an-1),数列{bn}的通项公式为bn=4n+3;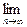
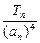

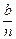 元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.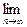 Pn(b).
Pn(b).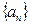 的前n项和为
的前n项和为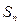 ,对于任意正整数n,都有等式:
,对于任意正整数n,都有等式: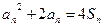 成立,求
成立,求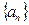 的通项an.
的通项an.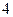 个实数
个实数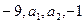 成等差数列,
成等差数列,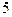 个实数
个实数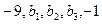 成等比数列,
成等比数列,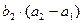 .
.