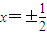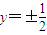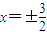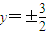题目内容
已知双曲线的方程为x2-
思路分析:由弦长公式|AB|=![]() ·
·![]() ,但必须先求出k值.
,但必须先求出k值.
设直线l的方程,利用OA⊥OB求出k值,即得|AB|的长度.
解:双曲线x2-![]() =1的右焦点F(2,0).
=1的右焦点F(2,0).
则过右焦点的直线l的方程为y=k(x-2).
由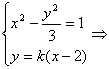 (3-k2)x2+4k2x-(4k2+3)=0.
(3-k2)x2+4k2x-(4k2+3)=0.
设A(x1,y1)、B(x2,y2),
则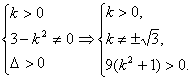
∴k∈R+且k≠-![]() .
.
由韦达定理得x1+x2=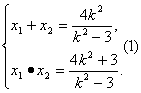
又∵![]() ,则x1x2+y1y2=0.
,则x1x2+y1y2=0.
由A、B两点都在l:y=k(x-2)上,则
y1·y2=k2(x1-2)(x2-2)
=k2[x1x2-2(x1+x2)+4],
由y1y2=-x1x2,则(k2+1)x1x2-2k2(x1+x2)+4k2=0. (2)
将(1)代入(2)中得
(k2+1)·![]() -2k2·
-2k2·![]() +4k2=0.
+4k2=0.
∴5k2=3.
∴k=±![]() .
.
又∵k>0,∴k=![]() .
.
∴|AB|=![]() ·
·![]()
=![]()
=![]() ·
·![]() =
=![]() =4.
=4.
∴|AB|=4.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
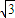 y=0和x+
y=0和x+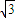 y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )
y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )