题目内容
给出以下结论:①函数y=2x与函数y=log2x的图象关于y轴对称;
②
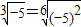 ;
;③函数y=ln(1+x)-ln(1-x)为奇函数;
④函数f(x)的定义域为[-1,4],则函数f(x2)的定义域为[-2,2]
其中正确的是 .
【答案】分析:根据函数与反函数图象间的关系可得①不正确;利用根式的运算法则可得②不正确;根据函数的奇偶性的判断方法可得③正确;根据函数的定义域的
定义可得④正确,从而得出结论.
解答:解:由于函数y=2x与函数y=log2x的互为反函数,故它们的图象关于直线y=x对称,故①不正确.
由于 <0,而
<0,而 =
=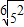 >0,∴
>0,∴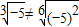 ,故②不正确.
,故②不正确.
由于函数y=f(x)=ln(1+x)-ln(1-x)的定义域为(-1,1),关于原点对称,且f(-x)=ln(1-x)-ln(1+x)=-f(x),
故函数y=ln(1+x)-ln(1-x)为奇函数,故③正确.
由于函数f(x)的定义域为[-1,4],可得-1≤x2≤4,解得-2≤x≤2,则函数f(x2)的定义域为[-2,2],故④正确.
故答案为 ③④.
点评:本题主要考查函数与反函数图象间的关系、根式的运算法则、函数的奇偶性、函数的定义域,属于基础题.
定义可得④正确,从而得出结论.
解答:解:由于函数y=2x与函数y=log2x的互为反函数,故它们的图象关于直线y=x对称,故①不正确.
由于
 <0,而
<0,而 =
=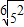 >0,∴
>0,∴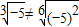 ,故②不正确.
,故②不正确.由于函数y=f(x)=ln(1+x)-ln(1-x)的定义域为(-1,1),关于原点对称,且f(-x)=ln(1-x)-ln(1+x)=-f(x),
故函数y=ln(1+x)-ln(1-x)为奇函数,故③正确.
由于函数f(x)的定义域为[-1,4],可得-1≤x2≤4,解得-2≤x≤2,则函数f(x2)的定义域为[-2,2],故④正确.
故答案为 ③④.
点评:本题主要考查函数与反函数图象间的关系、根式的运算法则、函数的奇偶性、函数的定义域,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 已知函数f(x)的导函数f'(x)的图象如图所示,给出以下结论:
已知函数f(x)的导函数f'(x)的图象如图所示,给出以下结论: