Question

如图2-4-7,AB和AC与⊙O相切于B、C,P是⊙O上一点,且PE⊥AB于E,PD⊥BC于D,PF⊥AC于F.求证:PD ²= PE·PF.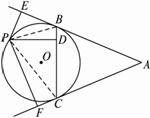

图2-4-7

Answer 1

思路解析:由结论先想到证△PDE∽△PFD,但这两个三角形相似的条件不够,注意到图中有切线AB、AC,构造弦切角.

证明:连结PB、PC.?

∵AB切⊙O于B,则∠PBE =∠PCD.?

又∵PE⊥AB,PD⊥BC,?

∴∠PEB=∠PDC=90°.?

∴△PBE∽△PCD.?

∴=.?

∵AC切⊙O于C,?

∴∠PCF =∠PBD.?

又∵PF⊥AC,PD⊥BC,?

∴∠PFC =∠PDB =90°.?

∴△PBD∽△PCF.?

∴=.

∴=.?

∴PD² =PE·PF.