题目内容
如图2-4-7,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,弦BD∥XY,AC、BD相交于点E.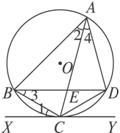
图2-4-7
(1)求证:△ABE≌△ACD;
(2)若AB=6 cm,BC=4 cm,求AE的长.
思路分析:第(1)问中的全等已经具备了AB=AC,再利用弦切角定理与圆周角定理可以得角的相等关系;对于(2),则利用△BCE∽△ACB建立比例式,解方程获得AE的长.
(1)证明:∵XY是⊙O的切线,∴∠1=∠2.
∵BD∥XY,
∴∠1=∠3.∴∠2=∠3.
∵∠3=∠4,∴∠2=∠4.
∵∠ABD=∠ACD,又∵AB=AC,∴△ABE≌△ACD.
(2)解:∵∠3=∠2,∠BCE=∠ACB,∴△BCE∽△ACB.
∴![]() .
.
∴AC·CE=BC2,即AC·(AC-AE)=BC2.
∵AB=AC=6,BC=4,∴6(6-AE)=16.
∴AE=![]() (cm).
(cm).
深化升华 本题利用平行线、弦切角、圆周角等进行了角的转换,利用相似建立方程求线段的长度,综合应用时,必须非常熟悉图形中的各个量,盯准要求的数值,向图形和已知索取条件.

练习册系列答案
相关题目
现有A、B两个班级,每个班级各有45名学生参加一次测验,每名参加者可获得0,1,2,3,4,5,6,7,8,9分这几种不同分值中的一种,A班的测试结果如下表所示:
分数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数 | 1 | 3 | 5 | 7 | 6 | 8 | 6 | 4 | 3 | 2 |
B班的成绩如图2-2-16所示.
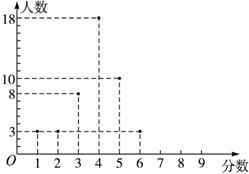
图2-2-16
(1)你认为哪个班级的成绩比较稳定?
(2)若两班共有60人及格,则参加者最少获得多少分才可能及格?
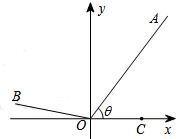 如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高.
如图,已知点A(3,4),C(2,0),点O为坐标原点,点B在第二象限,且|OB|=3,记∠AOC=θ.高. 如图,已知集合A={2,3,4,5,6,8},B={1,3,4,5,7},C={2,4,5,7,8,9},用列举法写出图中阴影部分表示的集合为
如图,已知集合A={2,3,4,5,6,8},B={1,3,4,5,7},C={2,4,5,7,8,9},用列举法写出图中阴影部分表示的集合为 (2013•广州二模)一个圆锥的正(主)视图及其尺寸如图2所示.若一个平 行于圆锥底面的平面将此圆锥截成体积之比为l:7的上、下两部分,则截面的面积为.
(2013•广州二模)一个圆锥的正(主)视图及其尺寸如图2所示.若一个平 行于圆锥底面的平面将此圆锥截成体积之比为l:7的上、下两部分,则截面的面积为.