题目内容

如图2-5-13,PA切⊙O于A,割线PBC交⊙O于B、C两点,D为PC的中点,连结AD并延长交⊙O于E,已知BE2＝DE·EA,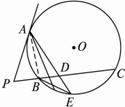

图2-5-13

求证:（1）PA＝PD;

（2）BP2＝AD·DE.

思路分析:（1）中因为PA与PD在同一个三角形中,所以可以通过说明两角相等解决问题;（2）中则运用切割线定理转换线段.

证明:(1)连结AB,证明△BED∽△AEB得∠DBE＝∠DAB.?

又可证∠PAD＝∠ADP,?

∴PA＝PD.?

(2)PA2＝PB·PC且PD ＝CD ＝?,PA ＝PD,?

∴PD＝2PB＝PB+BD.?

∴PB＝BD＝.?

又BD·CD＝AD·DE,?

∴可证得结论,且PD ＝CD.

练习册系列答案
相关题目
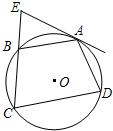精英家教网下列四个命题中，真命题的序号有
 
（写出所有真命题的序号）．
①将函数y=|x+1|的图象按向量y=（-1，0）平移，得到的图象对应的函数表达式为y=|x|．
②圆x2+y2+4x-2y+1=0与直线y=
1
2
x相交，所得弦长为2．
③若sin（α+β）=
1
2
，sin（α-β）=
1
3
，则tanαcotβ=5．
④如图，已知正方体ABCD-A1B1C1D1，P为底面ABCD内一动点，P到平面AA1D1D的距离与到直线CC1的距离相等，则P点的轨迹是抛物线的一部分．
精英家教网A．如图，四边形ABCD内接于⊙O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
求证：AB2=BE•CD．
B．已知矩阵M
2-3
1-1
所对应的线性变换把点A（x，y）变成点A′（13，5），试求M的逆矩阵及点A的坐标．
C．已知圆的极坐标方程为：ρ2-4
2
ρcos(θ-
π
4
)+6=0．
（1）将圆的极坐标方程化为直角坐标方程；
（2）若点P（x，y）在该圆上，求x+y的最大值和最小值．
D．解不等式|2x-1|＜|x|+1．
下列四个命题中，真命题的序号有
①③④
①③④
（写出所有真命题的序号）．
①两个相互垂直的平面，一个平面内的任意一直线必垂直于另一平面内的无数条直线．
②圆x2+y2+4x+2y+1=0与直线y=
1
2
x相交，所得弦长为2．
③若sin（α+β）=
1
2
，sin（α-β）=
1
3
，则tanαcotβ=5．
④如图，已知正方体ABCD-A1B1C1D1，P为底面ABCD内一动点，P到平面AA1D1D的距离与到直线CC1的距离相等，则P点的轨迹是抛物线的一部分．
（考生注意：从下列三题中任选一题，多选的只按照第一题计分）
①对任意x∈R，|2-x|+|3+x|≥a2-4a恒成立，则a满足
[-1，5]
[-1，5]
．
②在极坐标系中，点P（2，-
π
6
）到直线l：ρsin（θ-
π
6
）=1的距离是
3
+1
3
+1
；
③如图，点P在圆O直径AB的延长线上，且PB=OB=2，PC切圆O于点C，CD⊥AB于点D，则CD=
3
3
．
（2012•江苏）A．[选修4-1：几何证明选讲]
如图，AB是圆O的直径，D，E为圆上位于AB异侧的两点，连接BD并延长至点C，使BD=DC，连接AC，AE，DE．
求证：∠E=∠C．
B．[选修4-2：矩阵与变换]
已知矩阵A的逆矩阵A-1=
-
1
4
3
4
1
2
-
1
2
，求矩阵A的特征值．
C．[选修4-4：坐标系与参数方程]
在极坐标中，已知圆C经过点P（
2
，
π
4
），圆心为直线ρsin（θ-
π
3
）=-
3
2
与极轴的交点，求圆C的极坐标方程．
D．[选修4-5：不等式选讲]
已知实数x，y满足：|x+y|＜
1
3
，|2x-y|＜
1
6
，求证：|y|＜
5
18
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网