题目内容
已知函数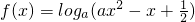 在x∈(1,2]上的函数值恒为正数,则实数a的取值范围是________.
在x∈(1,2]上的函数值恒为正数,则实数a的取值范围是________.
a> 或0<a<
或0<a<
分析:欲使函数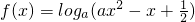 在x∈(1,2]上的函数值恒为正数,就a的值分情况讨论,转化成
在x∈(1,2]上的函数值恒为正数,就a的值分情况讨论,转化成 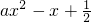 >1(或<1)在x∈(1,2]上的恒成立,根据函数
>1(或<1)在x∈(1,2]上的恒成立,根据函数 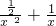 在(1,2]上的单调性求出最大(小)值即可得到实数a的取值范围.
在(1,2]上的单调性求出最大(小)值即可得到实数a的取值范围.
解答:欲使函数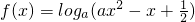 在x∈(1,2]上的函数值恒为正数,
在x∈(1,2]上的函数值恒为正数,
(1)当a>1时,转化成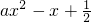 >1在x∈(1,2]上的恒成立,
>1在x∈(1,2]上的恒成立,
即a>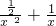
由于函数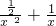 在(1,2]上的最大值为
在(1,2]上的最大值为 ,
,
∴a> ;
;
(2)当0<a<1时,转化成0<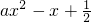 <1在x∈(1,2]上的恒成立,
<1在x∈(1,2]上的恒成立,
即a<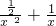 且a>
且a>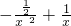
由于函数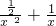 在(1,2]上的最小值为
在(1,2]上的最小值为 ,
,
且函数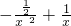 在(1,2]上的最大值为
在(1,2]上的最大值为
∴ <a<
<a< ;
;
综上所述,实数a的取值范围是:a> 或
或 <a<
<a< .
.
点评:本题主要考查了二次函数恒成立问题,以及函数的单调性等有关基础知识,同时考查了分析问题解决问题的能力,属于中档题.
 或0<a<
或0<a<
分析:欲使函数
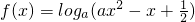 在x∈(1,2]上的函数值恒为正数,就a的值分情况讨论,转化成
在x∈(1,2]上的函数值恒为正数,就a的值分情况讨论,转化成 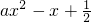 >1(或<1)在x∈(1,2]上的恒成立,根据函数
>1(或<1)在x∈(1,2]上的恒成立,根据函数 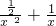 在(1,2]上的单调性求出最大(小)值即可得到实数a的取值范围.
在(1,2]上的单调性求出最大(小)值即可得到实数a的取值范围.解答:欲使函数
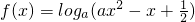 在x∈(1,2]上的函数值恒为正数,
在x∈(1,2]上的函数值恒为正数,(1)当a>1时,转化成
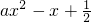 >1在x∈(1,2]上的恒成立,
>1在x∈(1,2]上的恒成立,即a>
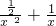
由于函数
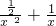 在(1,2]上的最大值为
在(1,2]上的最大值为 ,
,∴a>
 ;
;(2)当0<a<1时,转化成0<
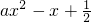 <1在x∈(1,2]上的恒成立,
<1在x∈(1,2]上的恒成立,即a<
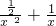 且a>
且a>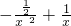
由于函数
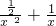 在(1,2]上的最小值为
在(1,2]上的最小值为 ,
,且函数
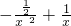 在(1,2]上的最大值为
在(1,2]上的最大值为
∴
 <a<
<a< ;
;综上所述,实数a的取值范围是:a>
 或
或 <a<
<a< .
.点评:本题主要考查了二次函数恒成立问题,以及函数的单调性等有关基础知识,同时考查了分析问题解决问题的能力,属于中档题.

练习册系列答案
相关题目
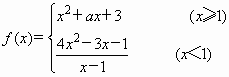 在x=1处连续,则a=
在x=1处连续,则a= 在x=1处有极值10.
在x=1处有极值10.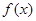 的单调区间;
的单调区间;